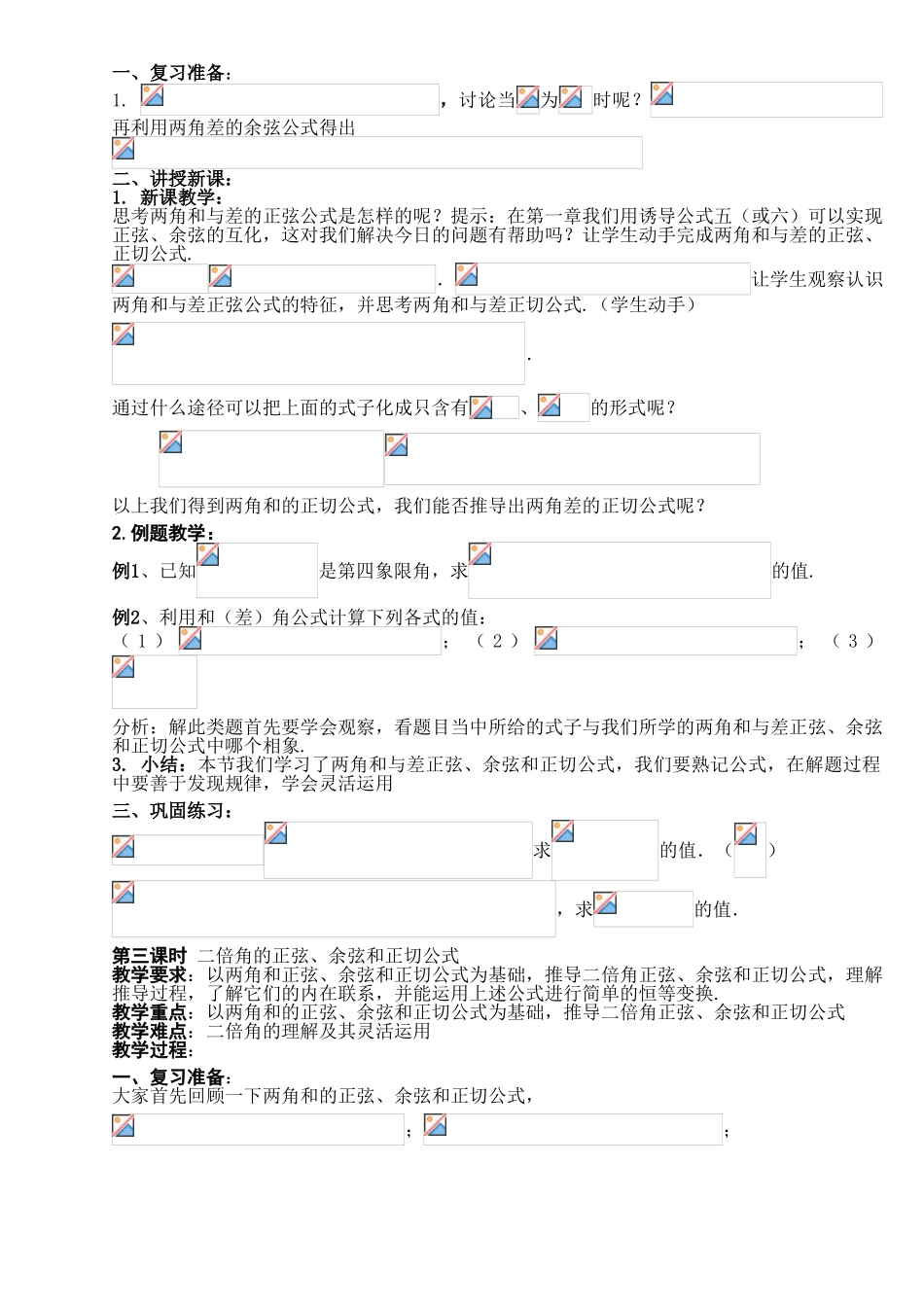
第一课时 两角差的余弦公式(一)教学要求:经历用向量的数量积推导出两角差的余弦公式的过程,进一步体会向量方法的作用教学重点:用向量的数量积推导出两角差的余弦公式教学难点:两角差的余弦公式的推导及运用教学过程:一、复习准备:1. 向量的知识:数量积; 二、讲授新课:1. 新课导入:①情景导入:我们在初中时就知道 ,,由此我们能否得到大家可以猜想,是不是等于呢?根据第一章所学的知识可知猜想是错误的!下面一起探讨两角差的余弦公式在第一章三角函数的学习当中我们知道,在设角的终边与单位圆的交点为,等于角与单位圆交点的横坐标,也可以用角的余弦线来表示,大家思考:怎样构造角和角?(注意:要与它们的正弦线、余弦线联系起来.)思考:我们在第二章学习用向量的知识解决相关的几何问题,两角差余弦公式我们能否用向量的知识来证明?提示:1、结合图形,明确应该选择哪几个向量,它们是怎样表示的?2、怎样利用向量的数量积的概念的计算公式得到探究结果?:记忆:右端为的同名三角函数积的和左端为两角差的余弦例1、利用余弦公式计算的值点评:把一个具体角构造成两个角的和、差形式,有很多种构造方法,要学会灵活运用. 例2、已知,是第三象限角,求的值.点评:注意角、的象限,也就是符号问题.3.小结:、的象限,也就是符号问题,学会灵活运用.三、巩固练习:1. 已知 2. 3. 作业:课本第150页第2、3、4题第二课时 两角和与差的正弦、余弦、正切公式教学要求:理解以两角差的余弦公式为基础,推导两角和、差正弦和正切公式的方法,体会三角恒等变换特点的过程,理解推导过程,掌握其应用.教学重点:两角和、差正弦和正切公式的推导过程及运用教学难点:两角和与差正弦、余弦和正切公式的灵活运用教学过程:一、复习准备:1. ,讨论当为时呢?再利用两角差的余弦公式得出二、讲授新课:1. 新课教学:思考两角和与差的正弦公式是怎样的呢?提示:在第一章我们用诱导公式五(或六)可以实现正弦、余弦的互化,这对我们解决今日的问题有帮助吗?让学生动手完成两角和与差的正弦、正切公式..让学生观察认识两角和与差正弦公式的特征,并思考两角和与差正切公式.(学生动手).通过什么途径可以把上面的式子化成只含有、的形式呢? 以上我们得到两角和的正切公式,我们能否推导出两角差的正切公式呢? 2.例题教学:例1、已知是第四象限角,求的值.例2、利用和(差)角公式计算下列各式的值:( 1 ); ( 2 ...