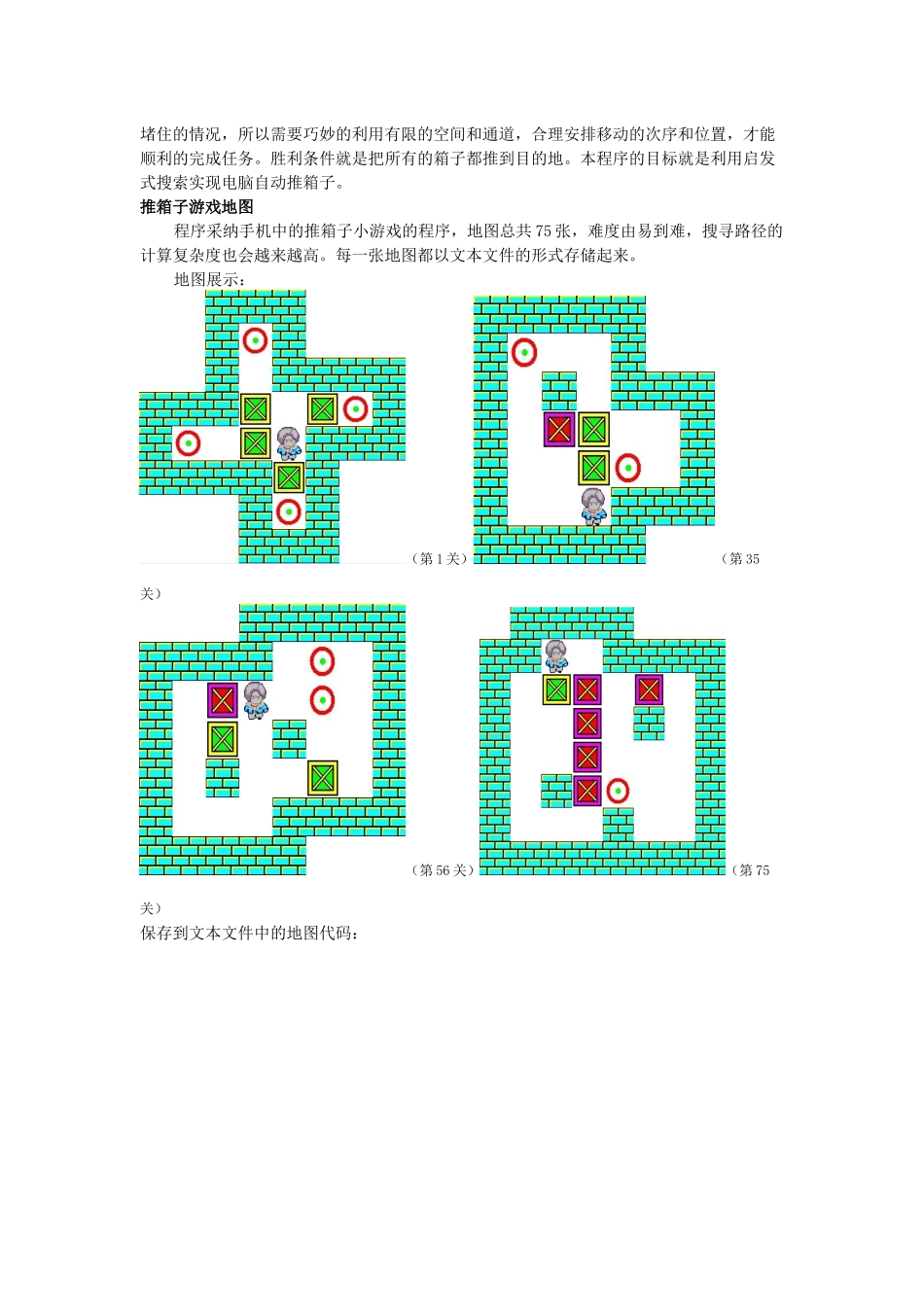
人工智能课程报告——推箱子小游戏的人工智能寻路 学院:姓名:学号:班级:指导老师: 人工智能课程报告一.简介推箱子游戏简介经典的推箱子是一个来自日本的古老游戏,目的是在训练你的逻辑思考能力。在一个狭小的仓库中,要求把木箱放到指定的位置,稍不小心就会出现箱子无法移动或者通道被堵住的情况,所以需要巧妙的利用有限的空间和通道,合理安排移动的次序和位置,才能顺利的完成任务。胜利条件就是把所有的箱子都推到目的地。本程序的目标就是利用启发式搜索实现电脑自动推箱子。推箱子游戏地图程序采纳手机中的推箱子小游戏的程序,地图总共 75 张,难度由易到难,搜寻路径的计算复杂度也会越来越高。每一张地图都以文本文件的形式存储起来。地图展示:(第 1 关)(第 35关)(第 56 关)(第 75关)保存到文本文件中的地图代码:推箱子中人的行为人只可以推箱子, 不可以拉, 而且一次只能推动一个。即使是处于目的位置的箱子也可以推走。二.基本概念启发式搜索考虑一个普通的图搜索问题:给出初始状态(节点 s)和目标状态(节点 t,可以不止一个)以及 状态的产生规则,求从 s 到 t 的一条路经。搜索过程可描述如下:1 待展开的节点集合(OPEN 表)为 {s},已展开的节点集合(CLOSED 表)为 {},节点 s 的层深为 g(s) = 0。2 每次从 OPEN 表中取出一个节点 n,根据规则扩展产生一组节点 mi,然后把 n 放入 CLOSED 表中。节点 mi 可能属于下列三种情况之一:(1)新的节点,则把 mi 的源标记为 n,层深 g(mi) = g(n) + 1,并放入 OPEN 表中。(2)已在 OPEN 表中存在的节点,并且层深 g(mi) > g(n) + 1,说明从 s 到 mi 并且经由 n 的路径要比先前搜索得到的路径要短。因此,把 mi 的源改记为 n,层深 g(mi) = g(n) + 1,仍放入 OPEN 表中。(3)已在 CLOSED 表中存在的节点,并且层深 g(mi) > g(n) + 1。同理,把 mi 的源改记为 n,层深 g(mi) = g(n) + 1,并从 CLOSED 表中取出重新放入 OPEN 表中,留待以后重新搜索计算 mi 的子节点的层深。3 不断重复上一步操作,直到满足下列条件之一:(1)n == t,搜索成功。(2)OPEN 表为空,搜索失败。在以上过程中,如何从 OPEN 表中选取待扩展的节点是关键。假如每次均选取层深 g(n) 最小的节点,以上过程就是宽度优先搜索;假如每次均选取层深 g(n) 最大的节点,以上过程 就是深度优...