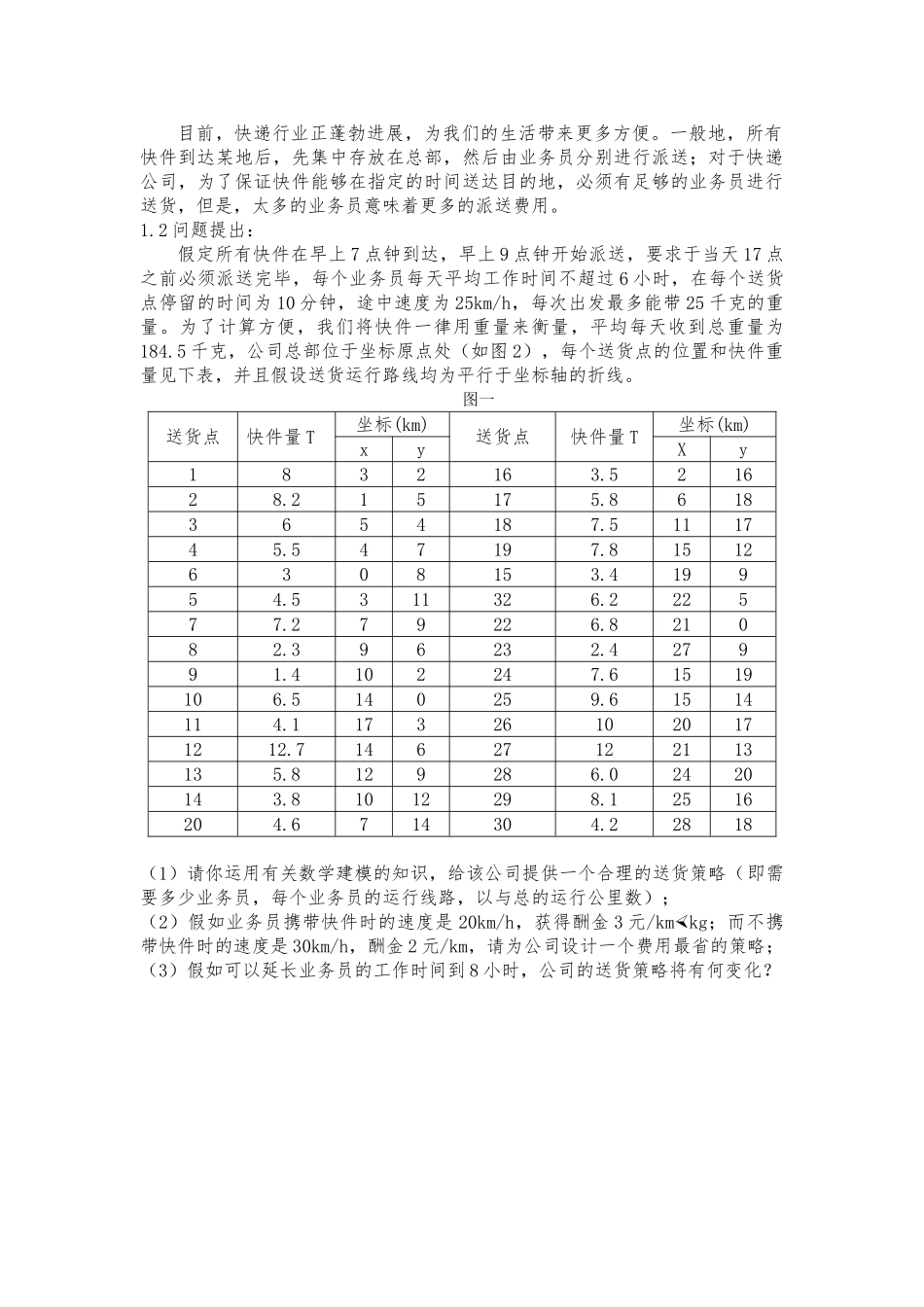
承 诺 书我们认真阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括、电子、网上咨询等)与队外的任何人(包括指导老师)讨论、讨论与赛题有关的问题。我们知道,抄袭别人的成果是违反竞赛规则的, 假如引用别人的成果或其他公开的资料(包括网上查到的资料),必须根据规定的参考文献的表述方式在正文引用处和参考文献中明确列出。我们重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。如有违反竞赛规则的行为,我们将受到严肃处理。我们参赛选择的题号是(从 A/B/C 中选择一项填写): C 我们的参赛报名号为(假如赛区设置报名号的话):所属学院(请填写完整的全名): 自动化 参赛队员 (打印并签名) :1. 2. 3. 日期:2013 年 8 月 23 日评阅编号(老师评阅时填写):快递公司送货策略摘要: 本文是关于如何优化快递公司送货策略的问题,即在给定送货地点和给定设计规的条件下,确定所需业务员人数,每个业务员的运行线路,总的运行公里数,以与费用最省的策略。 本文主要从最短路经和费用最省两个角度解决该问题。针对问题一,利用单目标 0-1 规划模型和最佳匹配的原理,将送货点抽象为顶点,由于街道和坐标轴平行,即任意两顶点之间都有路。在此模型中,将两 点 之 间 的 距 离 为 这 两 点 横 纵 坐 标 差 的 绝 对 值 之 和 。 比 如A(x1,y1),B(x2,y2)两点,则两点之间距离为 d=|x2-x1|+|y2-y1|。通过多目标动态规划找出初步路径,再通过 lingo 软件对各路径进行优化。通过分析,其模型结果为:共需要 5 名快递员。快递员 1: 0-29-28-30-23-15-0;快递员 2: 0-8-26-27-0;快递员 3: 0-19-24-25-0-1-6-5-2-0;快递员 4:0-16-17-18-20-0-3-7-4-0;快递员 5:0-9-11-21-22-10-0-12-13-14-0 路程为461km,所需总的时间为 23.44h。针对问题二,根据题意,建立单目标 0-1 整数规划的数学模型,然后用类似于问题一的方法,建立满足题意的目标函数以与约束条件,并求得最优结果。最后,对所求解的方案进行修改。所得结果为:快递员 1 走 0-1-3-8-13-0-25-26-0;快递员 2 走 0-2-4-7-14-0;快递员 3 走:0-6-5-20-18-30;快递员 4 走:0-10-11-21-23-0;快递员 5 走:0-16-17-24-28;快递员 6 走:0-22-29-0;快递员 7 走:0-9-12-19-0-15-27-0;所走路程为 616km,最少费用为 13830.7 元。针对问题...