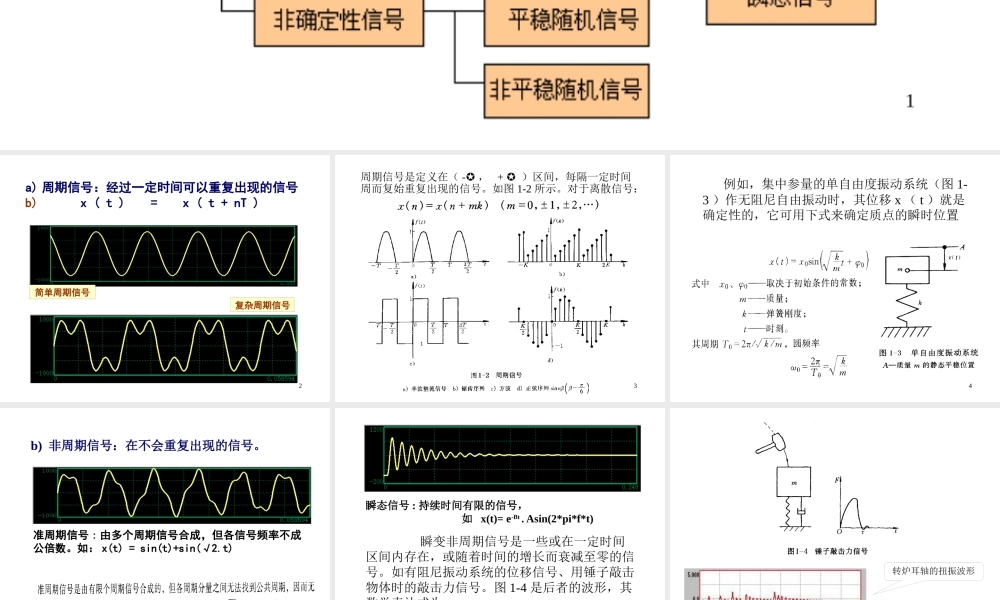
1.3.1 确定性信号与非确定性信号 可以用明确数学关系式描述的信号称为确定性信号。不能用数学关系式描述的信号称为非确定性信号。1a) 周期信号:经过一定时间可以重复出现的信号b) x ( t ) = x ( t + nT )简单周期信号复杂周期信号2周期信号是定义在( - , + )区间,每隔一定时间周而复始重复出现的信号。如图 1-2 所示。对于离散信号:3 例如,集中参量的单自由度振动系统(图 1-3 )作无阻尼自由振动时,其位移 x ( t )就是确定性的,它可用下式来确定质点的瞬时位置4b) 非周期信号:在不会重复出现的信号。 准周期信号 : 由多个周期信号合成,但各信号频率不成公倍数。如: x(t) = sin(t)+sin(√2.t)5瞬态信号 : 持续时间有限的信号, 如 x(t)= e-Bt . Asin(2*pi*f*t) 瞬变非周期信号是一些或在一定时间区间内存在,或随着时间的增长而衰减至零的信号。如有阻尼振动系统的位移信号、用锤子敲击物体时的敲击力信号。图 1-4 是后者的波形,其数学表达式为6转炉耳轴的扭振波形7c) 非确定性信号:不能用数学式描述,其幅值、相位变化不可预知,所描述物理现象是一种随机过程。 噪声信号 ( 平稳 )统计特性变异噪声信号 ( 非平稳 )8 随机信号任一次观测值只代表在其变化范围中可能产生的结果之一,但其值的变化服从统计规律,具有某些统计特征,可以用概率统计方法由其过去来估计其未来。 对随机信号按时间历程所作的各次长时间观测记录称为样本函数,记作 xi ( t ),如上图所示。在同一试验条件下,全部样本函数的集合(总体)就是随机过程,计作 x ( t ),即 x ( t ) = x1 ( t ), x2 ( t ), --- xi( t ) --- , 9 随机信号的各种统计值(均值、方差、均方值和均方根值等)是按集合平均来计算的。集合平均的计算不是沿某个样本的时间轴进行平均而是在集合中的某时刻 ti 对所有样本函数的观测值取平均。为了与集合平均相区别,称按单个样本的时间历程进行平均的计算为时间平均。 随机过程与样本函数102 能量信号与功率信号 a) 能量信号 在所分析的区间( -∞ ,∞),能量为有限值的信号称为能量信号,满足条件: dttx)(2一般持续时间有限的瞬态信号是能量信号。11b) 功率信号 在所分析的区间( -∞ ,∞),能量不是有限值.此时,研究信号的平均功率更为合适。 TTTTdttx)(l...