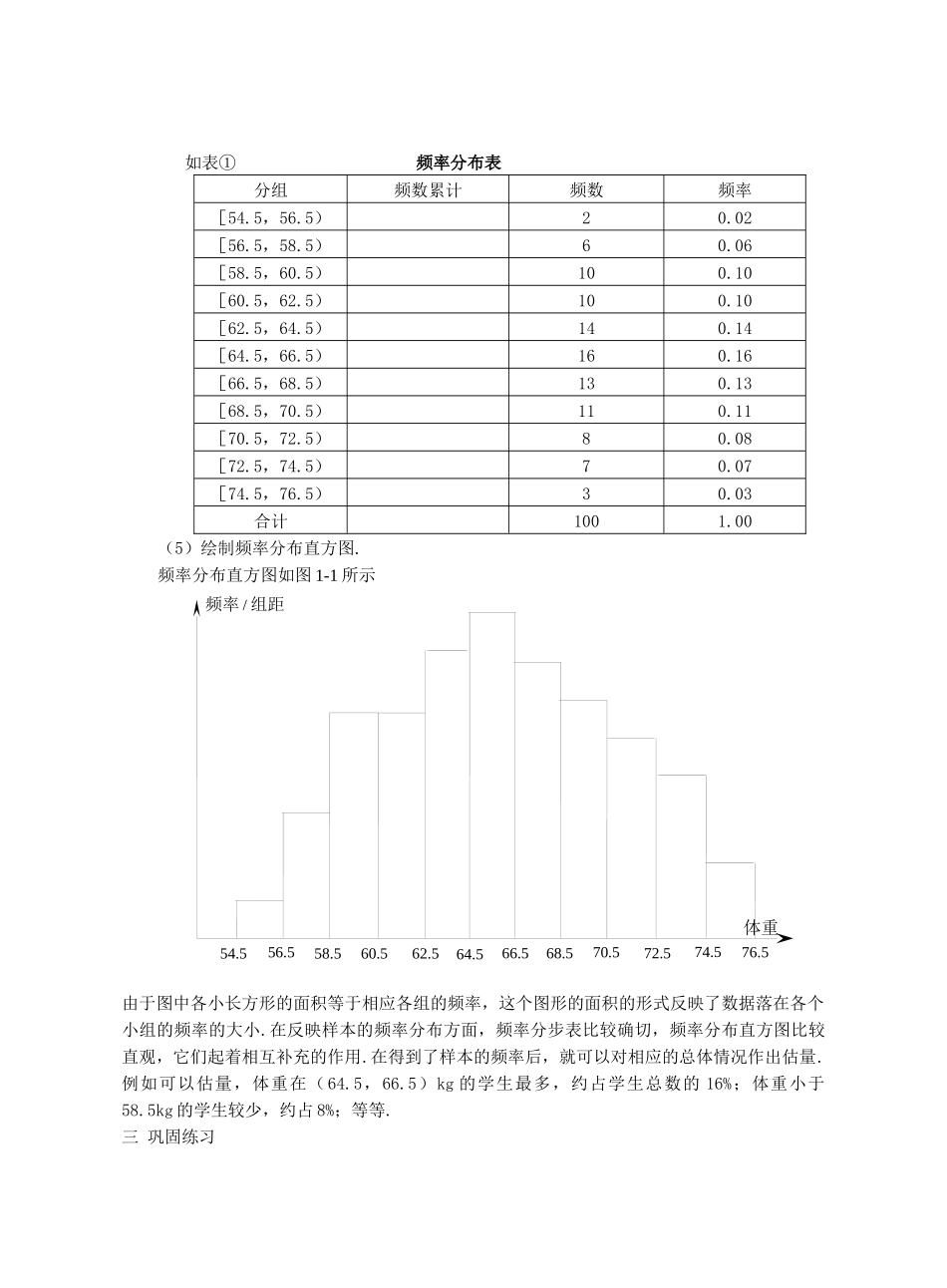
总体分布的估量(4 月 24 日)教学目标 通过统计案例,会用样本频率分布估量总体分布教学重点 用样本频率分布估量总体分布教学难点 频率分布表和频率分布直方图的绘制教学过程一 引入在统计中,为了考察一个总体的情况,通常是从总体中抽取一个样本,用样本的有关情况去估量总体的相应情况。这种估量大体分为两类,一类是用样本频率分布估量总体分布,一类是用样本的某种数字特征(例如平均数、方差等)去估量总体的相应数字特征。下面我们先通过案例来介绍总体分布的估量。二 案例分析例 1 为了了解某地区高三学生的身体发育情况,抽查了地区内 100 名年龄为 17.5 岁~18 岁的男生的体重情况,结果如下(单位:kg)56.569.56561.564.566.56464.57658.57273.556677057.565.56871756268.562.56659.563.564.567.57368557266.574636055.57064.5586470.55762.5656971.573625876716663.55659.563.5657074.568.56455.572.566.5687657.56071.55769.57464.55961.5676863.5585965.562.569.57264.575.568.5646265.558.567.570.5656666.5706359.5试根据上述数据画出样本的频率分布直方图,并对相应的总体分布作出估量。解:根据下列步骤获得样本的频率分布.(1)求最大值与最小值的差.在上述数据中,最大值是 76,最小值是 55,它们的差(又称为极差)是 76—55=21)所得的差告诉我们,这组数据的变动范围有多大.(2)确定组距与组数.假如将组距定为 2,那么由 21÷2=10.5,组数为 11,这个组数适合的.于是组距为 2,组数为 11.(3)决定分点.根据本例中数据的特点,第 1 小组的起点可取为 54.5,第 1 小组的终点可取为 56.5,为了避开一个数据既是起点,又是终点从而造成重复计算,我们规定分组的区间是“左闭右开”的.这样,所得到的分组是[54.5,56.5),[56.5,58.5),…,[74.5,76.5). (4)列频率分布表54.5频率 / 组距 56.558.574.572.566.568.570.576.562.560.564.5如表① 频率分布表分组频数累计频数频率[54.5,56.5)20.02[56.5,58.5)60.06[58.5,60.5)100.10[60.5,62.5)100.10[62.5,64.5)140.14[64.5,66.5)160.16[66.5,68.5)130.13[68.5,70.5)110.11[70.5,72.5)80.08[72.5,74.5)70.07[74.5,76.5)30.03合计1001.00(5)绘制频率分布直方图.频率分布直方图如图 1-1 所示由于图中各小长方形的面积等于相应各组的频率,这个图形的面积的形式反映了数据落在各个小组的频率的大小.在反映样本...