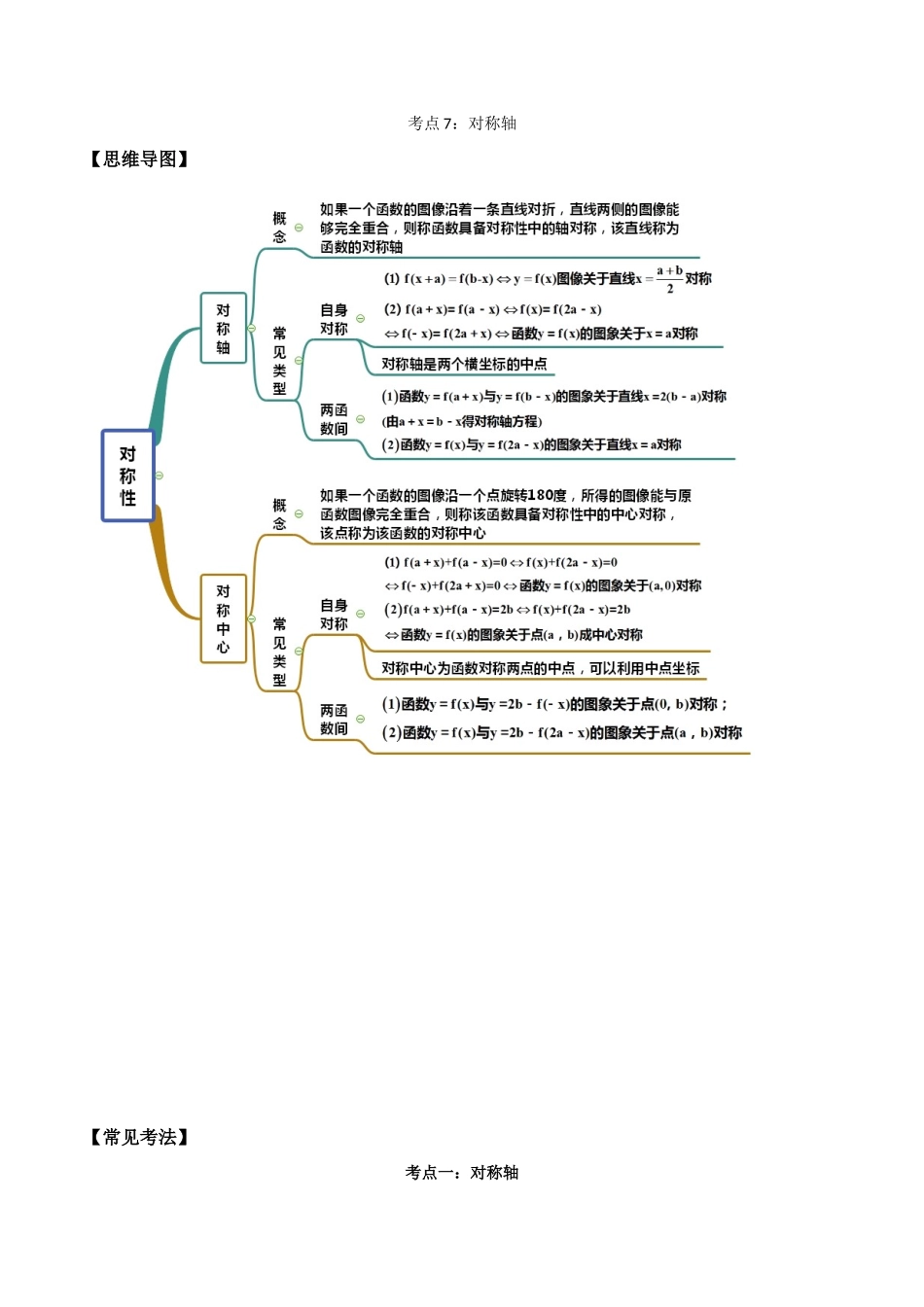
考点 7:对称轴【思维导图】【常见考法】考点一:对称轴1.定义域为的奇函数的图象关于直线对称,且,则 。【答案】2024【解析】因为函数的图像关于直线 x=2 对称,所以,所以所以,所以函数的周期是 8,所以.2.定义在 R 上的奇函数,满足,在区间上递增,则的大小关系 。【答案】【解析】因为,所以的图象关于直线 对称,由可知,又函数是 R 上的奇函数,所以 ,所以 ,即函数的周期 ,所以因为奇函数在区间上递增,所以在上递增, 因为的图象关于直线 对称,所以在上递减,所以.3.已知 f(x)在(0,2)上是增函数,f(x+2)是偶函数,的大小关系 。【答案】【解析】因为 f(x+2)是偶函数,所以函数关于直线对称,即.所以,,而 f(x)在(0,2)上是增函数,且 ,故.4.设函数的图像与的图像关于直线对称,且,则 。 【答案】2【解析】设是函数的图像上任意一点,它关于直线对称为(),由已知()在函数的图像上,∴,解得,即,∴,解得。5.已知函数 y=f(x)的图象与函数 y的图象关于原点对称,则 f(x)= .【答案】f(x)【解析】设是函数图象上的任意一点,它关于原点的对称点为,由题意在函数图象上,∴,即..考点二:对称中心1.已知偶函数的图象关于对称,且当时,,则时,= . 【答案】【解析】偶函数的图象关于对称则 得到,,故周期为 4设,则 2.已知函数对任意,都有的图象关于对称,且则 . 【答案】-4【解析】函数对任意,都有,,因此函数的周期,把的图象向左平移 1 个单位的的图象关于对称,因此函数为奇函数,.3 . 已 知 函 数的 图 象 关 于 原 点 对 称 , 且 满 足, 且 当时 ,,若,则 . 【答案】【解析】因为,故函数的周期为 4,则;而,由可得;而,解得.4.已知函数是定义在 R 上的奇函数,函数的图象与函数的图象关于直线对称,那么的对称中心为 . 【答案】【解析】函数是定义在 R 上的奇函数,则其图象关于原点对称由于函数的图象向左平移一个单位得到函数的图象则函数的图象关于对称又因为函数的图象与函数的图象关于直线对称所以函数的图象关于对称考点三:综合运用1 . 已 知 函 数的 定 义 域 为, 且 满 足 下 列 三 个 条 件 : ① 对 任 意 的, 都 有恒 成 立 ; ②; ③是 偶 函 数 . 若,,,则,,的大小关系正确的是 . 【答案】【解析】因为对任意的,都有恒成立,所以函数在上是增函数,由...