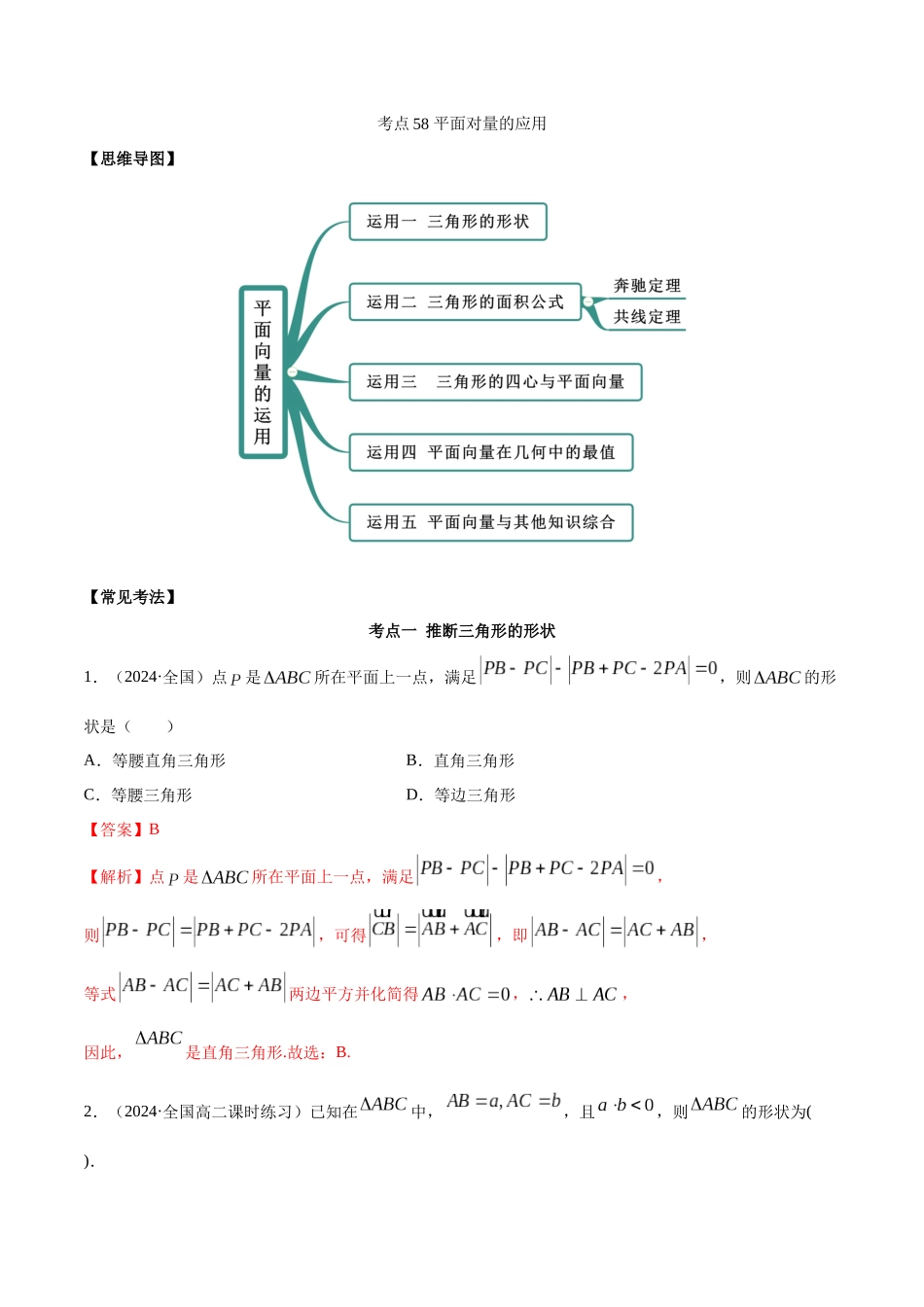
考点 58 平面对量的应用【思维导图】【常见考法】考点一 推断三角形的形状1.(2024·全国)点是所在平面上一点,满足,则的形状是( )A.等腰直角三角形B.直角三角形C.等腰三角形D.等边三角形【答案】B【解析】点是所在平面上一点,满足,则,可得,即,等式两边平方并化简得,,因此,是直角三角形.故选:B.2.(2024·全国高二课时练习)已知在中,,且,则的形状为( ).A.钝角三角形B.直角三角形C.锐角三角形D.等腰直角三角形【答案】A【解析】 ,∴∴90°<∠BAC<180°,故是钝角三角形. 答案为:A3.(2024·黑龙江青冈)已知是所在平面内一点,且满足,则为( )A.等腰三角形B.直角三角形C.等边三角形D.等腰直角三角形【答案】B【解析】因为,,因为,所以,因为,所以,由此可得以为邻边的平行四边形为矩形,所以,得的形状是直角三角形.4.(2024·重庆)若内有一点,满足,且,则一定是( )A.钝角三角形B.直角三角形C.等边三角形D.等腰三角形【答案】D【解析】因为,所以,所以,所以 O 在 AC的高线上,又,所以,设 AC 的中点为 D,所以,故 O 在 AC 的中线上,所以三角形一定是等腰三角形.选 D.考点二 三角形的面积(奔驰定理)1.(2024·恩施市第一中学)已知是三角形内部一点,且,则的面积与的面积之比为( )A.B.1C.D.2【答案】A【解析】由题意,是的重心,,所以的面积与的面积之比为.故选 A.2.(2024·四川涪城)如图所示,设 P 为所在平面内的一点,并且,则与的面积之比等于( )A.B.C.D.1【答案】C【解析】连接 CP 并延长交 AB 于 D, P、C. D 三点共线,∴,且,设,结合,得,由平面对量基本定理,解之得,且,∴,可得, 与有相同的底边 AB,高的比等于与之比,∴的面积与面积之比为.故选:C.3.已知 O 是内部一点,,且∠BAC=60°,则的面积为( )A.B.C.D.【答案】A【解析】 ,∴,∴为三角形的重心,∴的面积为面积的, ,∴, ,∴,的面积为,∴的面积为,故选 A.4.(2024·山东滨州.高三三模)已知点 O 是内一点,且满足,则实数 m 的值为( )A.B.C.2D.4【答案】D【解析】由得:设,则 三点共线如下图所示:与反向共线,, 故选:D.5.是内一点,满足,则( )A.B.C.D.【答案】B【解析】是内一点,且满足,.延长到,使得,延长到,使得,连结、、,则.是的重心,设,则,,,,.故选:.考点三 四心与平面对量1.(2024·...