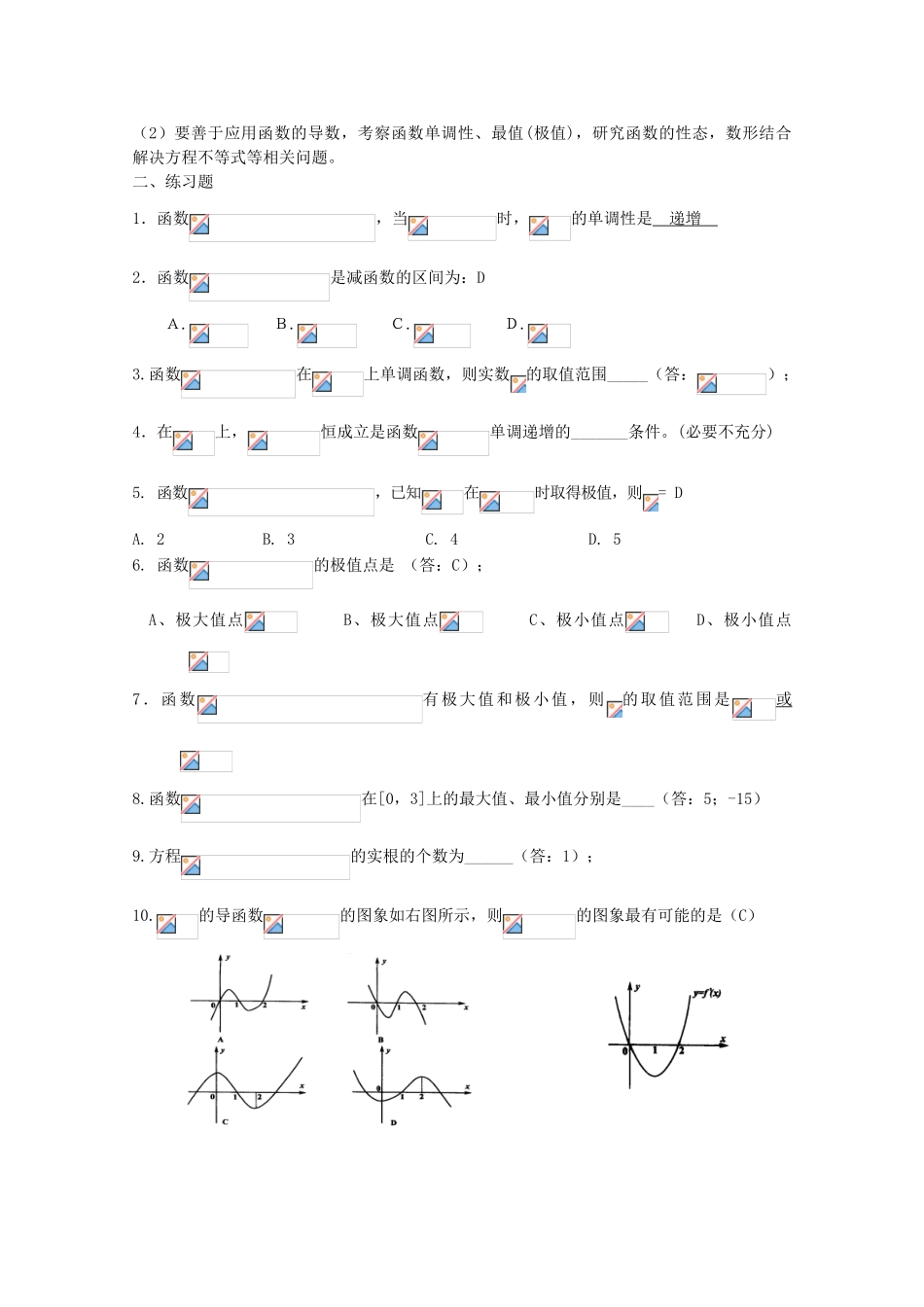
广东饶平二中 2011 高考第一轮学案:导数在研究函数中的运用一、知识与方法1、函数的单调性:若函数在区间()上单调递增,则,反之等号不成立;若函数在区间()上单调递减,则,反之等号不成立。2、函数的极值:(1)定义:设函数在点附近有定义,如果对附近所有的点,都有,就说是函数的一个极大值。记作=,如果对附近所有的点,都有,就说是函数的一个极小值。记作=。极大值和极小值统称为极值。(2)求函数在某个区间上的极值的步骤:( i)求导数;(ii)求方程的根;(iii)检查在方程的根的左右的符号:“左正右负”在处取极大值;“左负右正”在处取极小值。特别提醒:(1)是极值点的充要条件是点两侧导数异号,而不仅是=0;=0 是为极值点的必要而不充分条件。(2)给出函数极大(小)值的条件,一定要既考虑,又要考虑检验“左正右负”(“左负右正”)的转化,否则条件没有用完,这一点一定要切记!3、函数的最大值和最小值:(1)定义:函数在一闭区间上的最大值是此函数在此区间上的极大值与其端点值中的“最大值”;函数在一闭区间上的最小值是此函数在此区间上的极小值与其端点值中的“最小值”。(2)求函数在[]上的最大值与最小值的步骤:(i)求函数在()内的极值(极大值或极小值);(ii)将的各极值与,比较,其中最大的一个为最大值,最小的一个为最小值。特别注意:(1)利用导数研究函数的最值(极值),且方程在给定的范围内有多个值时,要注意列表!(2)要善于应用函数的导数,考察函数单调性、最值(极值),研究函数的性态,数形结合解决方程不等式等相关问题。二、练习题1.函数,当时,的单调性是 递增 2.函数是减函数的区间为:DA. B. C. D.3.函数在上单调函数,则实数的取值范围_____(答:);4.在上,恒成立是函数单调递增的_______条件。(必要不充分)5. 函数,已知在时取得极值,则= DA. 2B. 3C. 4D. 56. 函数的极值点是 (答:C);A、极大值点 B、极大值点 C、极小值点 D、极小值点7.函数有极大值和极小值,则的取值范围是或8.函数在[0,3]上的最大值、最小值分别是____(答:5;-15)9.方程的实根的个数为______(答:1);10.的导函数的图象如右图所示,则的图象最有可能的是(C) 11.已知函数的图象如右下图所示(其中是函数的导函数),下面四个图象中的图象大致是:C12. 若上是减函数,则 b 的取值范围是 CA. B. C. D.13. 函数在处有极小值 10,求的值.(答:...