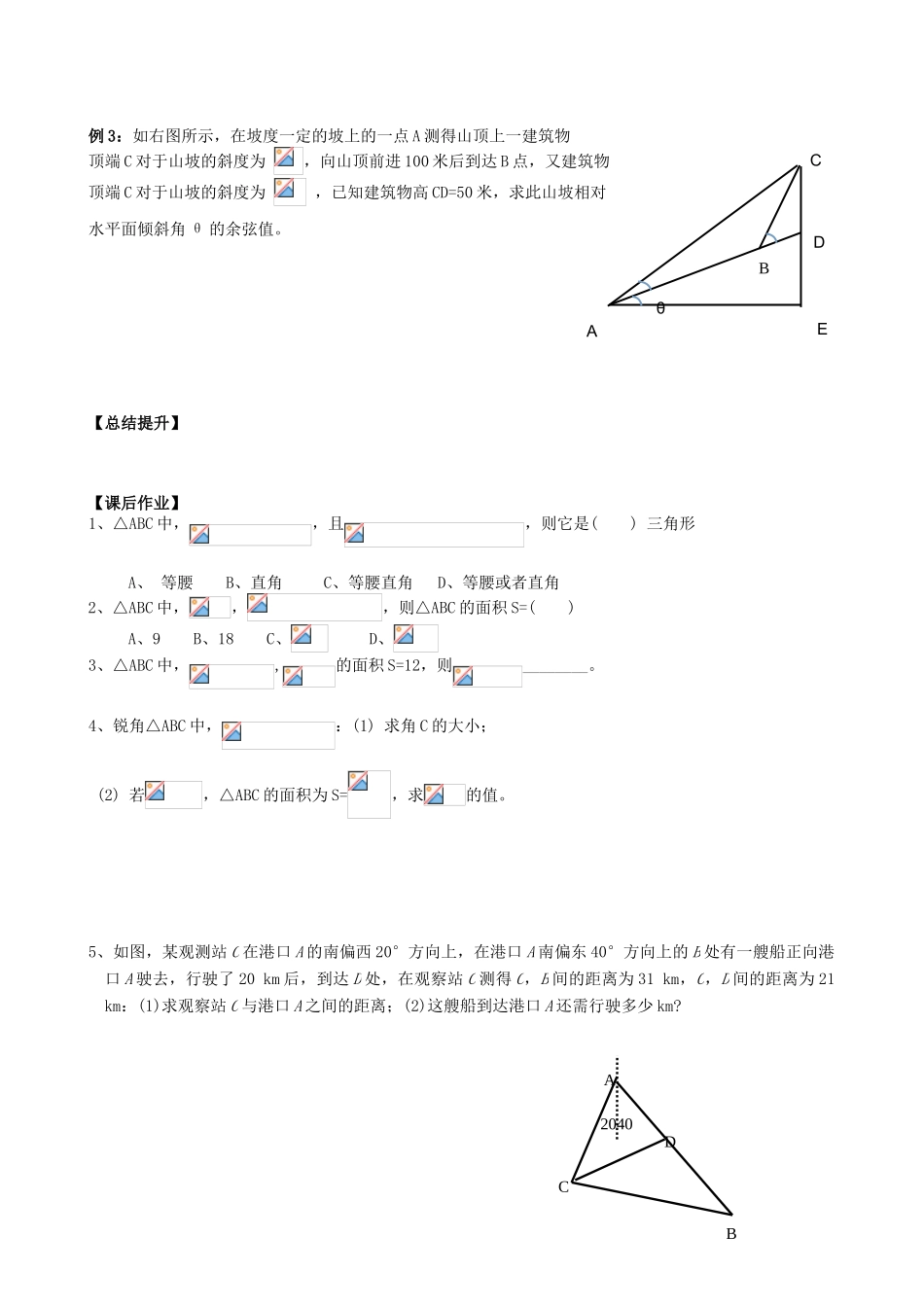
第一章《解三角形》全章复习【问题导学】阅读课本 P后回答下列问题:1、完成下表: 数学表达式 定理变形 定理的功能正弦定理余弦定理2、三角形的面积公式:_____________________________________________________________【基础自测】1、在△ABC 中,,则 ( ) A、 B、 C、 D、2、在△ABC 中,,则 ( ) A、 B、 C、 D、 3、在△ABC 中,,则____________。4、在△ABC 中,,则__________。5、在△ABC 中,,则△ABC 的面积 S=__________。【课内探究】例 1、在△ABC 中,若:(1) 求 B 的大小;(2) 若,求△ABC 的面积 S。例 2、在△ABC 中,若,,求角 A 及、的大小。例 3:如右图所示,在坡度一定的坡上的一点 A 测得山顶上一建筑物顶端 C 对于山坡的斜度为 ,向山顶前进 100 米后到达 B 点,又建筑物顶端 C 对于山坡的斜度为 ,已知建筑物高 CD=50 米,求此山坡相对水平面倾斜角 θ 的余弦值。 【总结提升】【课后作业】1、△ABC 中,,且,则它是( ) 三角形A、 等腰 B、直角 C、等腰直角 D、等腰或者直角2、△ABC 中,,,则△ABC 的面积 S=( )A、9 B、18 C、 D、3、△ABC 中,,的面积 S=12,则________。4、锐角△ABC 中,:(1) 求角 C 的大小; (2) 若,△ABC 的面积为 S=,求的值。5、如图,某观测站 C 在港口 A 的南偏西 20°方向上,在港口 A 南偏东 40°方向上的 B 处有一艘船正向港口 A 驶去,行驶了 20 km 后,到达 D 处,在观察站 C 测得 C,B 间的距离为 31 km,C,D 间的距离为 21 km:(1)求观察站 C 与港口 A 之间的距离;(2)这艘船到达港口 A 还需行驶多少 km? θBDCAEACDB2040