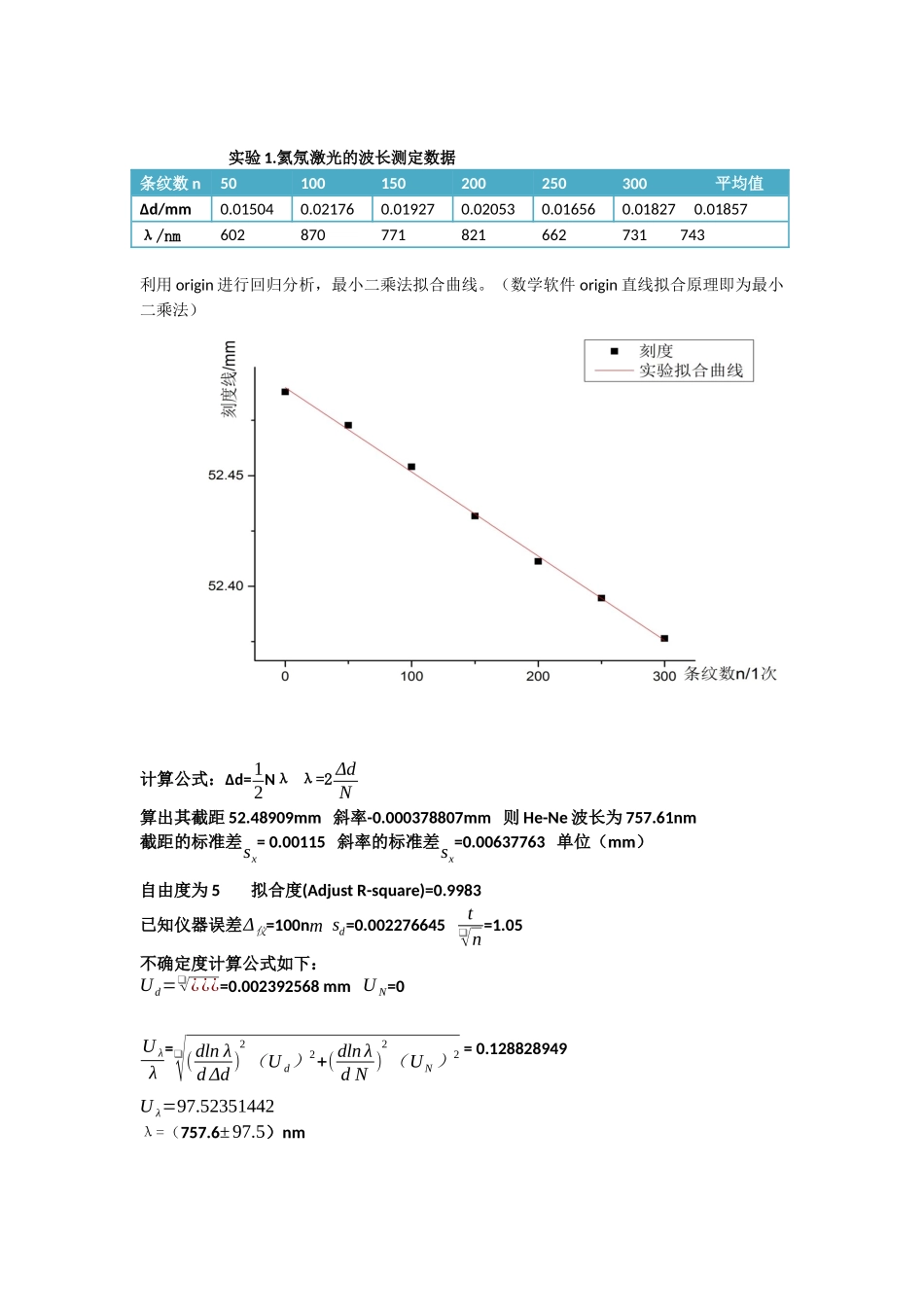
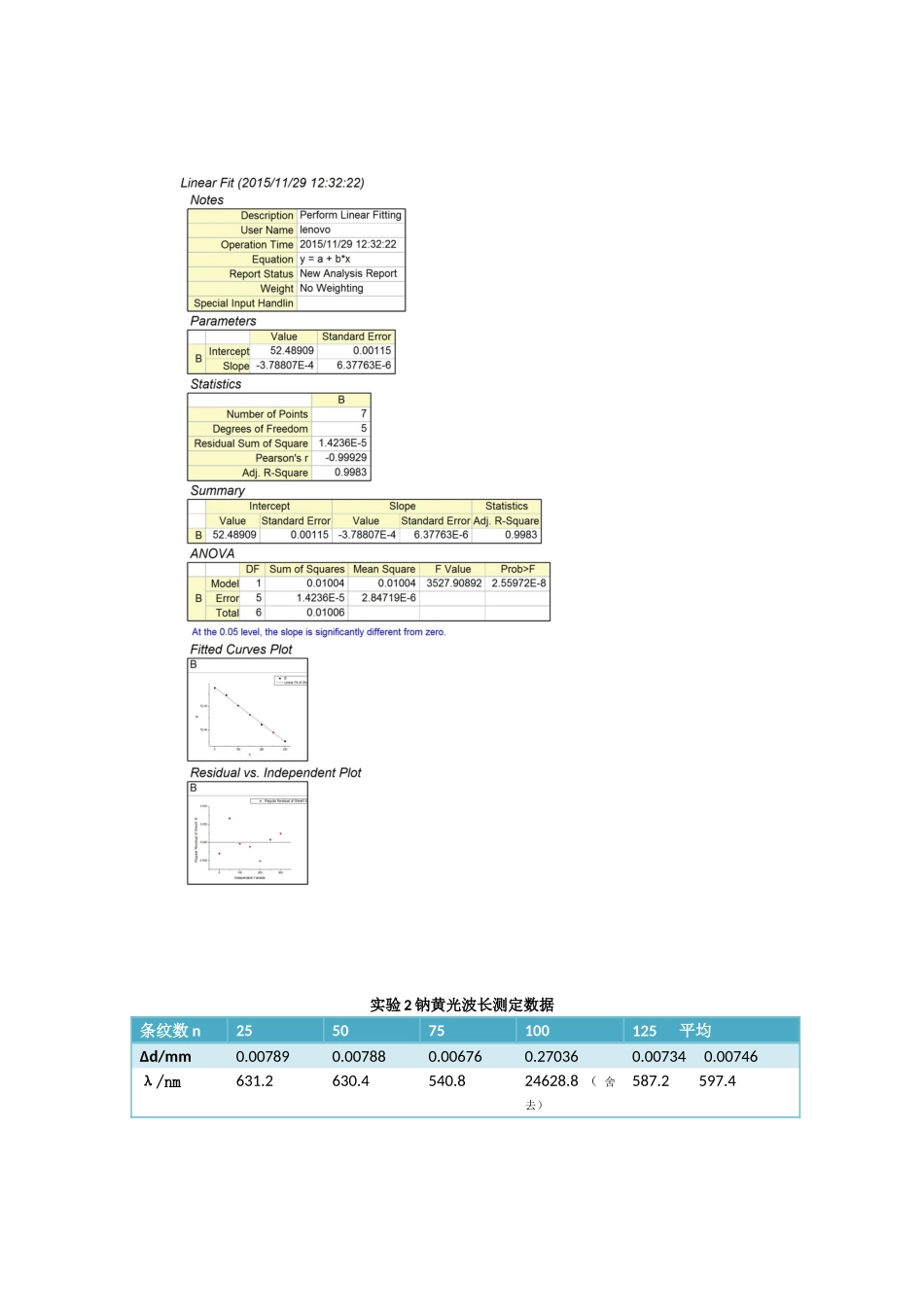
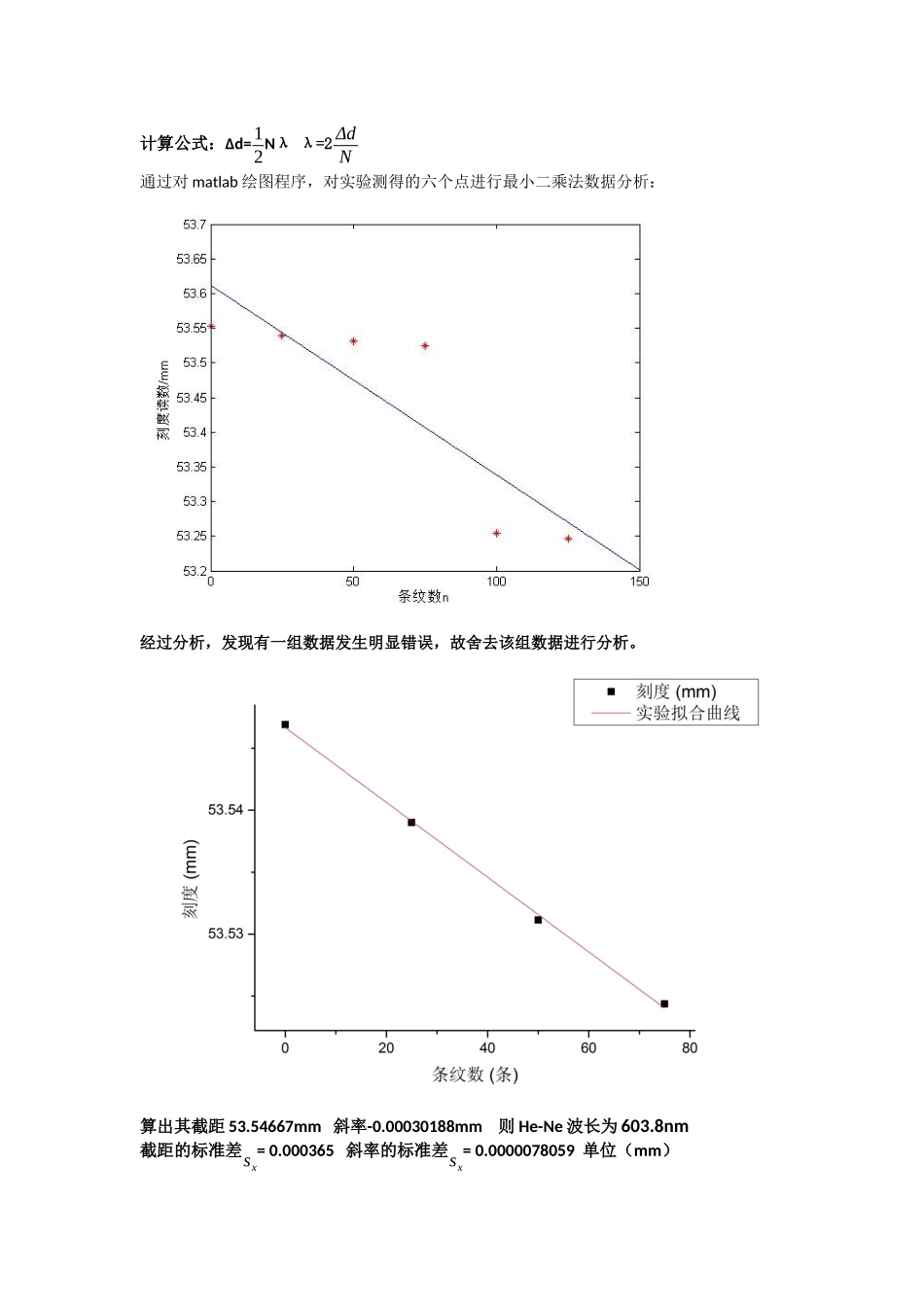
实验1.氦氖激光的波长测定数据条纹数n50100150200250300平均值Δd/mm0.015040.021760.019270.020530.016560.018270.01857λ/nm602870771821662731743利用origin进行回归分析,最小二乘法拟合曲线。(数学软件origin直线拟合原理即为最小二乘法)计算公式:Δd=12Nλλ=2ΔdN算出其截距52.48909mm斜率-0.000378807mm则He-Ne波长为757.61nm截距的标准差sx=0.00115斜率的标准差sx=0.00637763单位(mm)自由度为5拟合度(AdjustR-square)=0.9983已知仪器误差Δ仪=100nmsd=0.002276645t❑√n=1.05不确定度计算公式如下:Ud=❑√¿¿¿=0.002392568mmUN=0Uλλ=❑√(dlnλdΔd)2(Ud)2+(dlnλdN)2(UN)2=0.128828949Uλ=97.52351442λ=(757.6±97.5)nm实验2钠黄光波长测定数据条纹数n255075100125平均Δd/mm0.007890.007880.006760.270360.007340.00746λ/nm631.2630.4540.824628.8(舍去)587.2597.4计算公式:Δd=12Nλλ=2ΔdN通过对matlab绘图程序,对实验测得的六个点进行最小二乘法数据分析:经过分析,发现有一组数据发生明显错误,故舍去该组数据进行分析。算出其截距53.54667mm斜率-0.00030188mm则He-Ne波长为603.8nm截距的标准差sx=0.000365斜率的标准差sx=0.0000078059单位(mm)自由度为2拟合度(AdjustR-square)=0.998已知仪器误差Δ仪=100nmsd=0.000530346t❑√n=1.59不确定度计算公式如下:Ud=❑√¿¿¿=0.000849159mmUN=0Uλλ=❑√(dlnλdΔd)2(Ud)2+(dlnλdN)2(UN)2=0.113713902Uλ=68.66045377nmλ=(603.8±68.7)nm【实验讨论】:实验过程虽然比较简单,但是波长的测量等级达到了纳米级,仪器的误差达到了100nm,在测量过程中目测条纹变化数目有一定的观测误差,特别是在第二个实验中通过一块反射镜来观测条纹会产生较大误差,对记录人员也有一定的伤害,可以采用一块放大镜,方便读数。因为产生的干涉条纹是等倾条纹(同心圆),如果补偿板与分光板不严格平行;补偿板与分光板厚度不同都会导致呈椭圆状。使测量结果正确,必须避免引入空程误差,也就是说,在调整好零点以后,应将微动轮按原方向转几圈,直到干涉条纹开始移动以后,才可开始读数测量。【实验结论】:通过测量波长,学会掌握了迈克尔孙干涉仪的基本用法,了解了等倾条纹的形成特点,伴随光程差的变化,干涉条纹不停的“吞吐”条纹,使用了公式Δd=12Nλ,测量出He-Ne激光波长与钠黄灯波长。实验数据最后发现了有一定的误差,而且实验次数过少,误差也比较大,距离理想值有一定的差距,如果要增加精度应该再多次实验,可以改进方法,用测定双线波长差的方法计算波长。