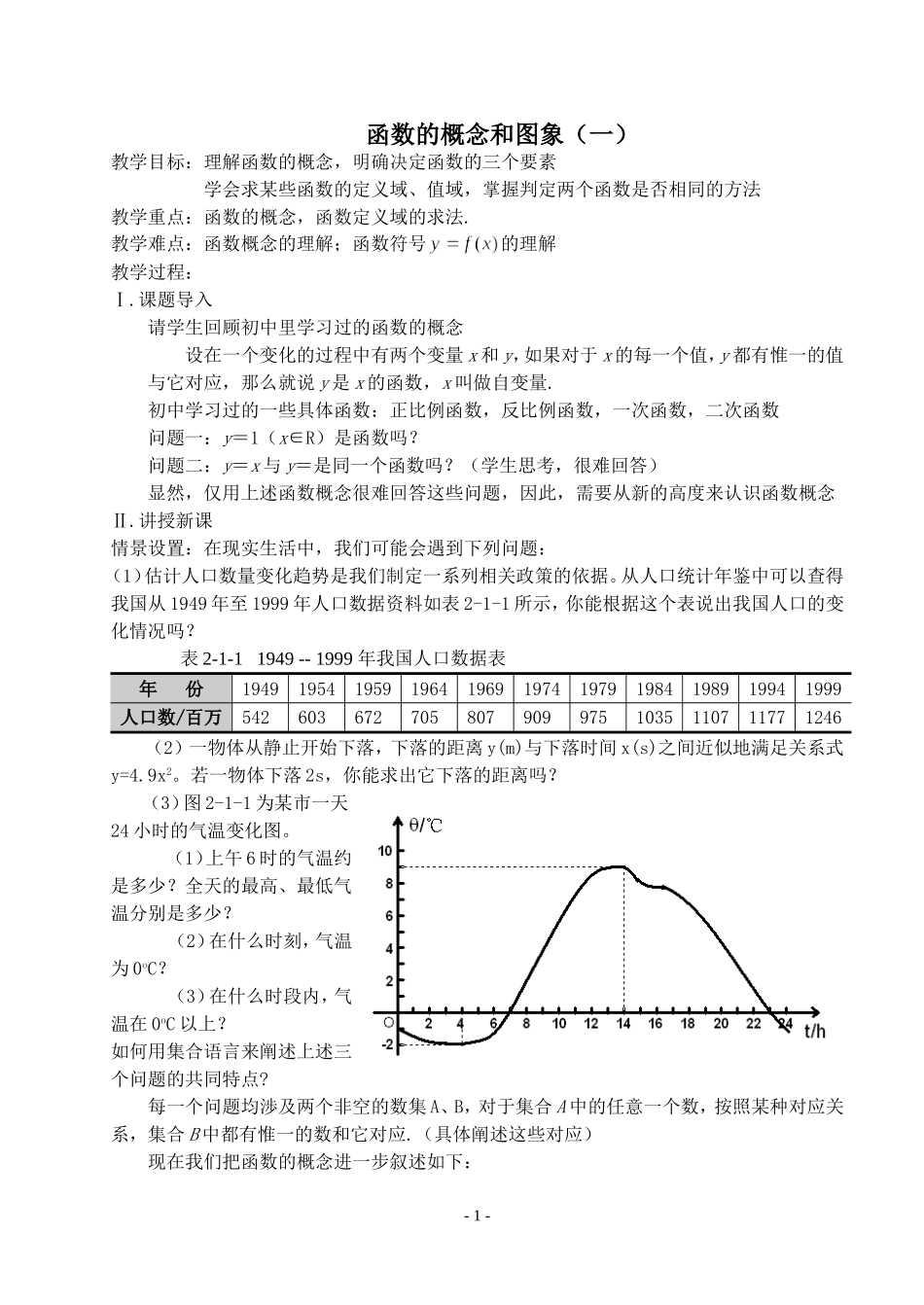
函数的概念和图象(一)教学目标:理解函数的概念,明确决定函数的三个要素学会求某些函数的定义域、值域,掌握判定两个函数是否相同的方法教学重点:函数的概念,函数定义域的求法.教学难点:函数概念的理解;函数符号的理解教学过程:Ⅰ.课题导入请学生回顾初中里学习过的函数的概念设在一个变化的过程中有两个变量 x 和 y,如果对于 x 的每一个值,y 都有惟一的值与它对应,那么就说 y 是 x 的函数,x 叫做自变量.初中学习过的一些具体函数:正比例函数,反比例函数,一次函数,二次函数问题一:y=1(x∈R)是函数吗?问题二:y=x 与 y=是同一个函数吗?(学生思考,很难回答)显然,仅用上述函数概念很难回答这些问题,因此,需要从新的高度来认识函数概念Ⅱ.讲授新课情景设置:在现实生活中,我们可能会遇到下列问题:(1)估计人口数量变化趋势是我们制定一系列相关政策的依据。从人口统计年鉴中可以查得我国从 1949 年至 1999 年人口数据资料如表 2-1-1 所示,你能根据这个表说出我国人口的变化情况吗? 表 2-1-1 1949 -- 1999 年我国人口数据表年 份19491954195919641969197419791984198919941999人口数/百万5426036727058079099751035110711771246(2)一物体从静止开始下落,下落的距离 y(m)与下落时间 x(s)之间近似地满足关系式y=4.9x2。若一物体下落 2s,你能求出它下落的距离吗?(3)图 2-1-1 为某市一天24 小时的气温变化图。(1)上午 6 时的气温约是多少?全天的最高、最低气温分别是多少?(2)在什么时刻,气温为 0oC?(3)在什么时段内,气温在 0oC 以上?如何用集合语言来阐述上述三个问题的共同特点?每一个问题均渉及两个非空的数集 A、B,对于集合 A 中的任意一个数,按照某种对应关系,集合 B 中都有惟一的数和它对应.(具体阐述这些对应)现在我们把函数的概念进一步叙述如下:- 1 -设 A、B 是非空的数集,如果按照某个确定的对应关系 f,使对于集合 A 中的任意一个数x,在集合 B 中都有惟一确定的数 f(x)和它对应,那么就称 f︰A→B 为从集合 A 到集合 B 的一个函数.记作:y=f(x),x∈A其中 x 叫自变量,x 的取值范围 A 叫做函数的定义域,与 x 的值相对应的 y(或 f(x))值叫做函数值,函数值的集合{y|y=f(x),x∈A}叫函数的值域.例如:(1)一次函数 f(x)=ax+b(a≠0)的定义域是 R,值域也是 R.对于 R 中的任意一个数 x,在 R 中...