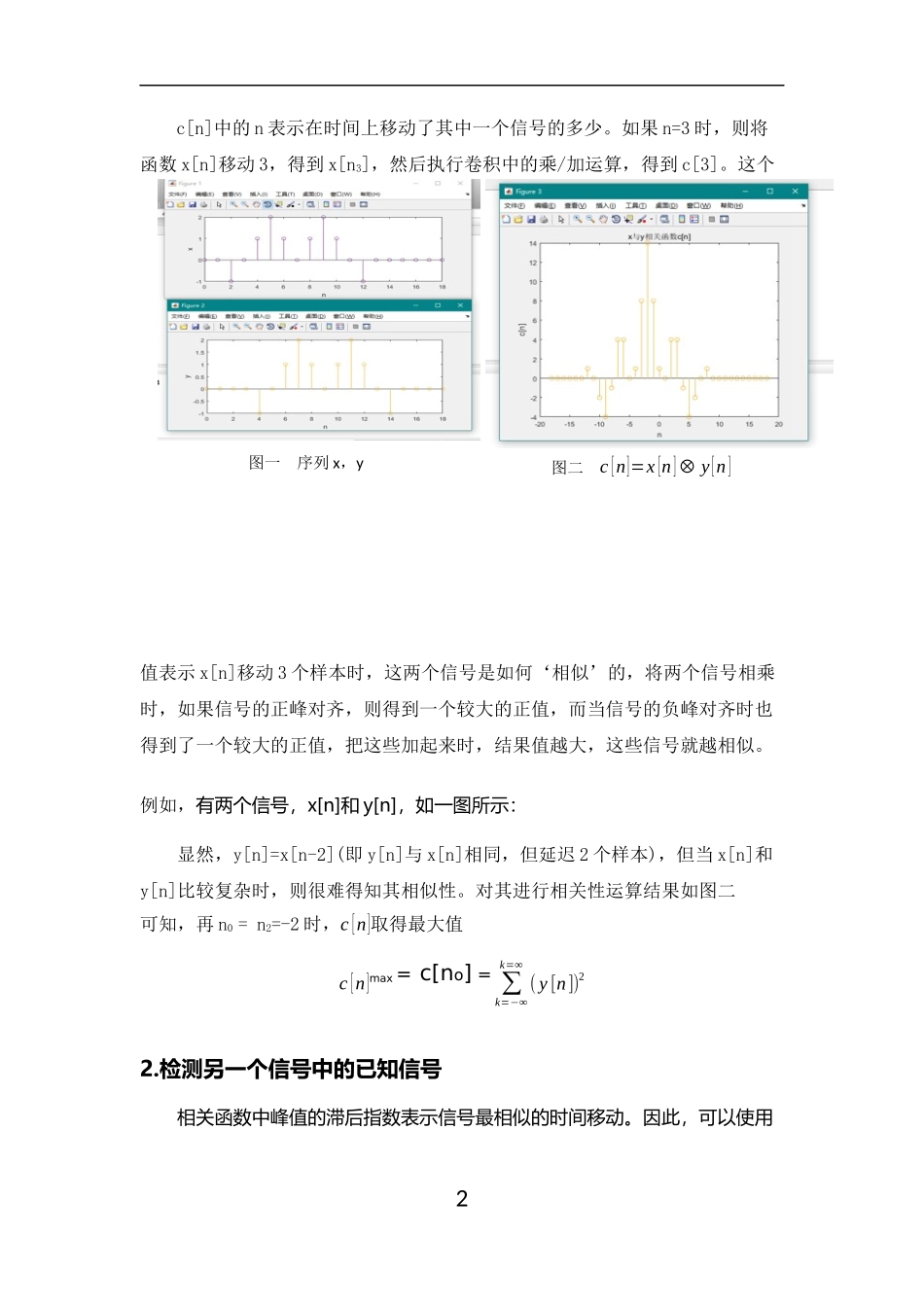
基于互相关的信号分析与应用在信号处理过程中,对两个信号的相似性的度量可以用相似性来表示。信号与自身的相关性称为自相关,两种信号的相关称为互相关。基于信号的相关性可以从未知信号中检测出目标信号。因此对信号相关性的研究具有重要意义。1.相关性的定义:在离散时间中,相关被定义为:c[n]=∑k=−∞k=∞x[n+k]y¿[k]=x[n]⊗y[n]其中,*表示复共轭,也可以表示为:[n]=cx[n]⊗y[n]=x[n]∗y¿[n]1c[n]中的n表示在时间上移动了其中一个信号的多少。如果n=3时,则将函数x[n]移动3,得到x[n3],然后执行卷积中的乘/加运算,得到c[3]。这个值表示x[n]移动3个样本时,这两个信号是如何‘相似’的,将两个信号相乘时,如果信号的正峰对齐,则得到一个较大的正值,而当信号的负峰对齐时也得到了一个较大的正值,把这些加起来时,结果值越大,这些信号就越相似。例如,有两个信号,x[n]和y[n],如一图所示:显然,y[n]=x[n-2](即y[n]与x[n]相同,但延迟2个样本),但当x[n]和y[n]比较复杂时,则很难得知其相似性。对其进行相关性运算结果如图二可知,再n0=n2=-2时,c[n]取得最大值c[n]max=c[no]=∑k=−∞k=∞(y[n])22.检测另一个信号中的已知信号相关函数中峰值的滞后指数表示信号最相似的时间移动。因此,可以使用2图一序列x,y图二c[n]=x[n]⊗y[n]相关性来检测某个信号c否包含在另一个信号中,如果是的话,则两个信号的互相关有一个很高的峰值.如果没有一个相对较高的峰值,则这些信号实际上没有任何时间延迟。例如,有一段几个人的声音的混合音频,用单个人的音频波形与混合波形进行互相关运算结果如图三:图三从图中所示的互相关函数的最大振幅来看,语音1、语音4和语音5出现在混合语音信号中。相应的C1[n],c4[n]和c5[n]函数有较高的峰。3.频域互相关我们现在很清楚,时间域的卷积与频域上的乘法是等价的。既然互相关可以用卷积来表示,其中:c[n]=x[n]∗y¿[−n]=x[n]⊗y[n]令DTFT{y[n]}=Y(e−jω)则,DTFT{y¿[−n]}=Y¿(e−jω)DTFT{y[−n]}=Y(e−jω)C(ejω)=X(ejω)Y¿(ejω)通过信号时域与频域之间的关系,可以DFFT和IDFFT很容易地计算出两个信号的相关性。如果,两个信号x、y的长度N1和N2不相等,则需要通过补零的方式将两信号长度变为N1+N2-1。例如,有两长度不相等的信号Xm、Y,利用信3号时域与频域之间的关系检测两信号的相关性,如图四。图四4.目标检测与距离估计利用互相关可以探测出附近的目标,并且可以估算出目标的距离。将一已知信号作为雷达信号,如果雷达信号遇到目标,则会有信号反射回信号接收设备。但是,接收到的返回信号可能会与雷达信号不同(如信号含有延时、噪声等)例如,返回信号(ReceivedSignal)包含雷达信号(TransmittedSignal)和其他信号(OtherSignal1、OtherSignal2)如图五。4图五假设返回的信号为x[n]=r[n]+n[n],其中s(t)为雷达探测信号,n[n]为噪声信号。将ReceivedSignal和TransmittedSignal进行相关性运算,即y[n]=x[n]⊗r[n],如果y[n]最大值显著高于其他,则可以确定x[n]中含有r[n],结果如图六。图六同理,将ReceivedSignal分别与OtherSignal1、OtherSignal2进行相关性运算,结果如图七。5图七显然,ReceivedSignal中存在TransmittedSignal、OtherSignal2,从图像中容易发现发射的信号似乎在n=400处出现在接收到的信号中,若已知雷达波速为光速(3*108m/s),频率为100KHz,接收到反馈信号时间延时为:400∗1s100000=4ms可以估计出目标的距离是:0.5∗0.004∗3∗108=600(Km)互相关在图像信号处理中的应用在观测场景r(x,y)=s(x,y)+n(x,y)中已知的目标图像s(x,y),其中n(x,y)表示噪声信号,与处理声音信号类似,通过求r(x,y)与已知目标图像s(x,y)互相关函数c(x,y)。然后,找到相关输出的一个峰值,如果这个峰值是超过一定的阈值,则可以认为该场景包含的目标是集中在峰值的位置。例如观测到的图像为图八,将图中A提取出来如图九,求出A的自相关函数并用图形表示如图十,求与的互相关c(x,y)并用matlab显示,如图十一。最后将所有与图具有相关条件的图形加框,如图十二。6图八图九图十7图十一图十二总结:由信号的相关性可知,相...