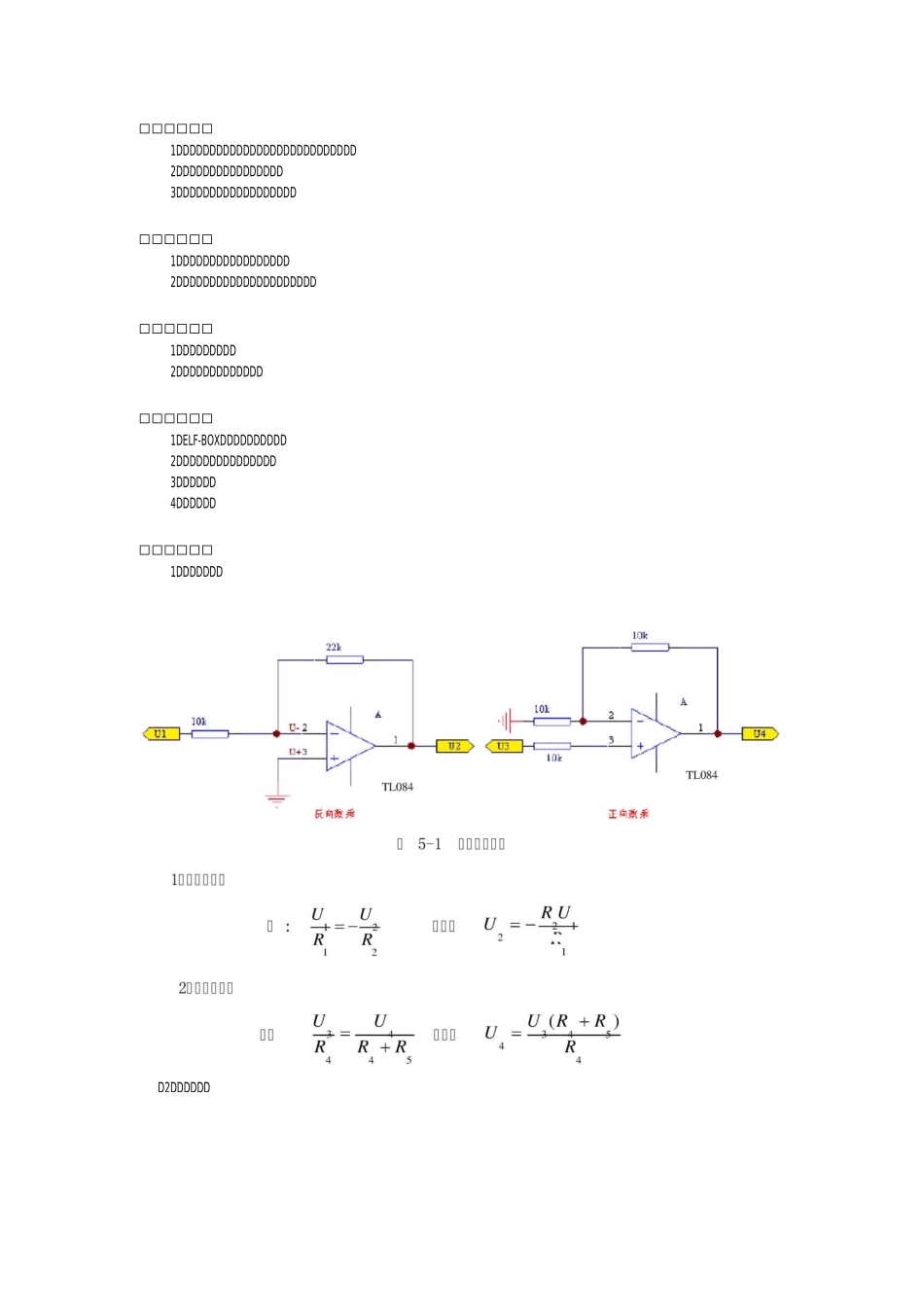
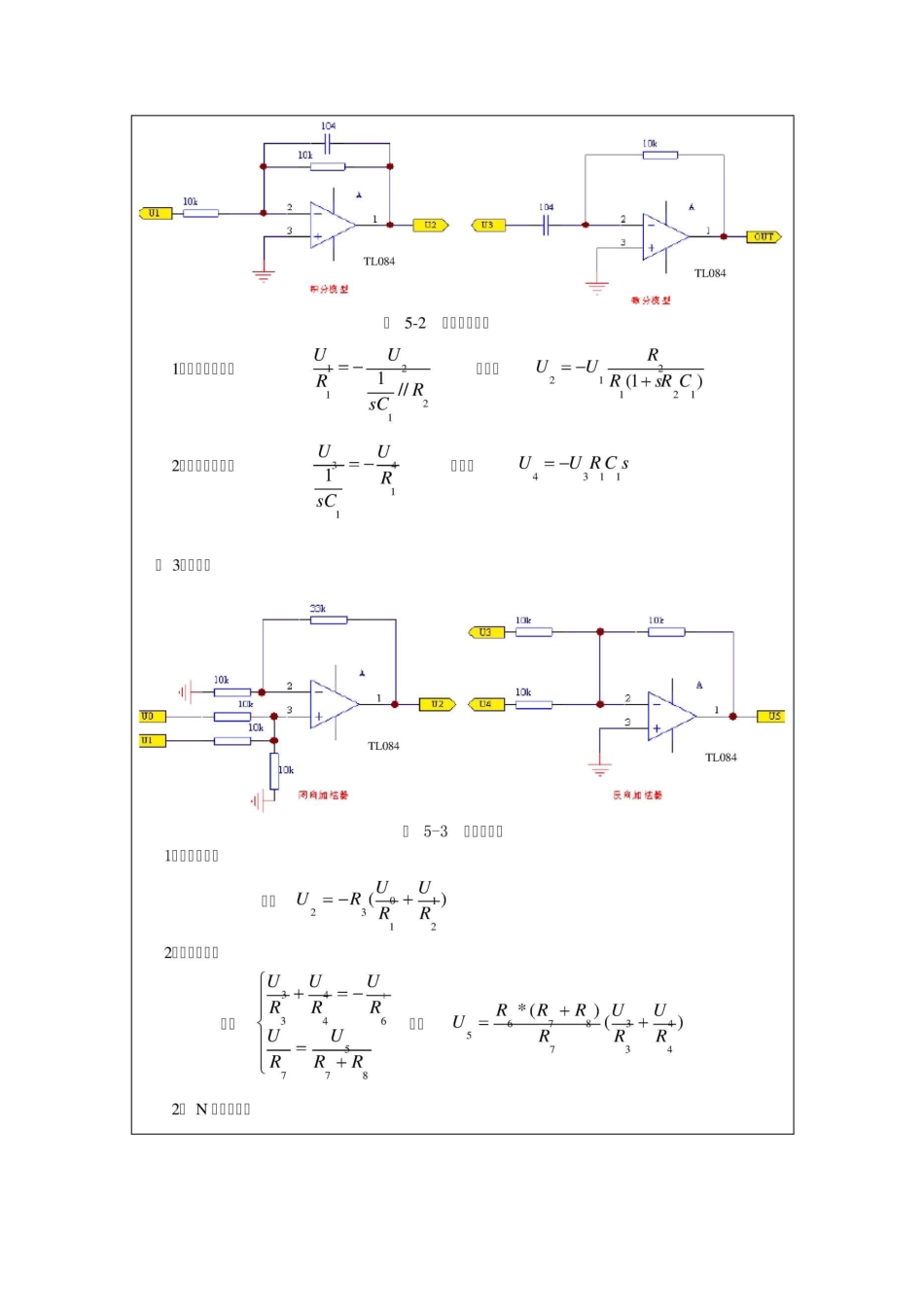
DDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDD2019D5D20DDDDDDDDDDDDD2019D5D24DDDD□□□□RD2DDDDDD□□□□□□1DDDDDDDDDDDDDDDDDDDDDDDDDDD2DDDDDDDDDDDDDDDD3DDDDDDDDDDDDDDDDDD□□□□□□1DDDDDDDDDDDDDDDDD2DDDDDDDDDDDDDDDDDDDDD□□□□□□1DDDDDDDDD2DDDDDDDDDDDDD□□□□□□1DELF-BOXDDDDDDDDDD2DDDDDDDDDDDDDDD3DDDDDD4DDDDDD□□□□□□1DDDDDDDD1DDDDDdndn-1dC—y(t)+C-y(t)++C-y(t)+Cy(t)=0dtn1dtn-1n-1dtndmdm-1•…dEx(t)+Ex(t)++Ex(t)+Ex(t)根据零状态响应(起始状态为零),则对其进行拉氏变换CsnY(s)+Csn-1Y(s)++CsY(s)+CY(s)二01n-1nEsmX(s)+Esm-1X(s)++EsX(s)+EX(s)01m-1m则其传函数可表达为:...H(s)Y(s)Esm+Esm-1+二一01X(s)Csn+Csn-1+01+Es+Em-1m+Cs+Cn-1n3、作为一阶系统,一般可表达一阶系统是构成复杂系统的基本单元,本实验提供搭建的电路为图 5-4。Es+E=—01Cs+C01学习一阶的特点有助于对一般系统特性的了解。其其传递函数表示为:H0—1+sTR—2R1则系统的频响特性为:H0——1+阿在搭建时要进行元件的参数的合理设计,实验中可以改变其参数,或者根据其传递函数,设计出其它的一阶网络系统。4、作为二阶系统,其一般可表达为:…、Es2+Es+EH(s)二 012图 5-4 一阶系统分析Cs2+Cs+C012其传KTT~12 丄丄 Ks2+Ts+—1TT其T=RCT=RC111222与标准的二阶系统比32H(s)=井"nTT=2—4TK1① 为无阻尼自然频率,g 为二阶系统的阻尼系数。通过改变图 5-5 中的电阻 R,即可改变系统的阻尼系数。在搭建时要进行元件的参数的合理设计,实验中可以改变其参数,或者根据其传递六、实验步在一阶系统的基础上,它又多了一个系统极点,本实验提供搭建的电路如下图 5-5:图 5-5 二阶系统分析1DDDDDDDDDDDD1DELF-BOXDDDDDDDDDDDDDDDDDDDDDDDDDUSBODDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDD+12VD-12VDGNDDDDDDDDDDDDD2DDDDDDD5-4DDDDDDDDDDDDDDDDDDDDDD二 R 二 10KD2DDDDDDDDDD0V-5VDDDDDDDDDDDDDDDTL084ODD1DDDDDDDDDDDDDDTL084DDDDDDDDDD5-7ODDOulpuljinvertinginputNcn-invertngInpir'VccNcn-irNerljngInpul2flvertinginput2□ilpul2匚匚OutputimerringinputJMcn-imertingIrpildVcNcn-irwerlingInpJ3invertinginput3□Utp.ltD5-7D3DDDDDD1DDDD-12v+12V 叮口POWER_OFFDPOWER_ONUDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDPOWER_ONDPOWER_OFFDDDD+12V-12VDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDD...