5函数单调性1

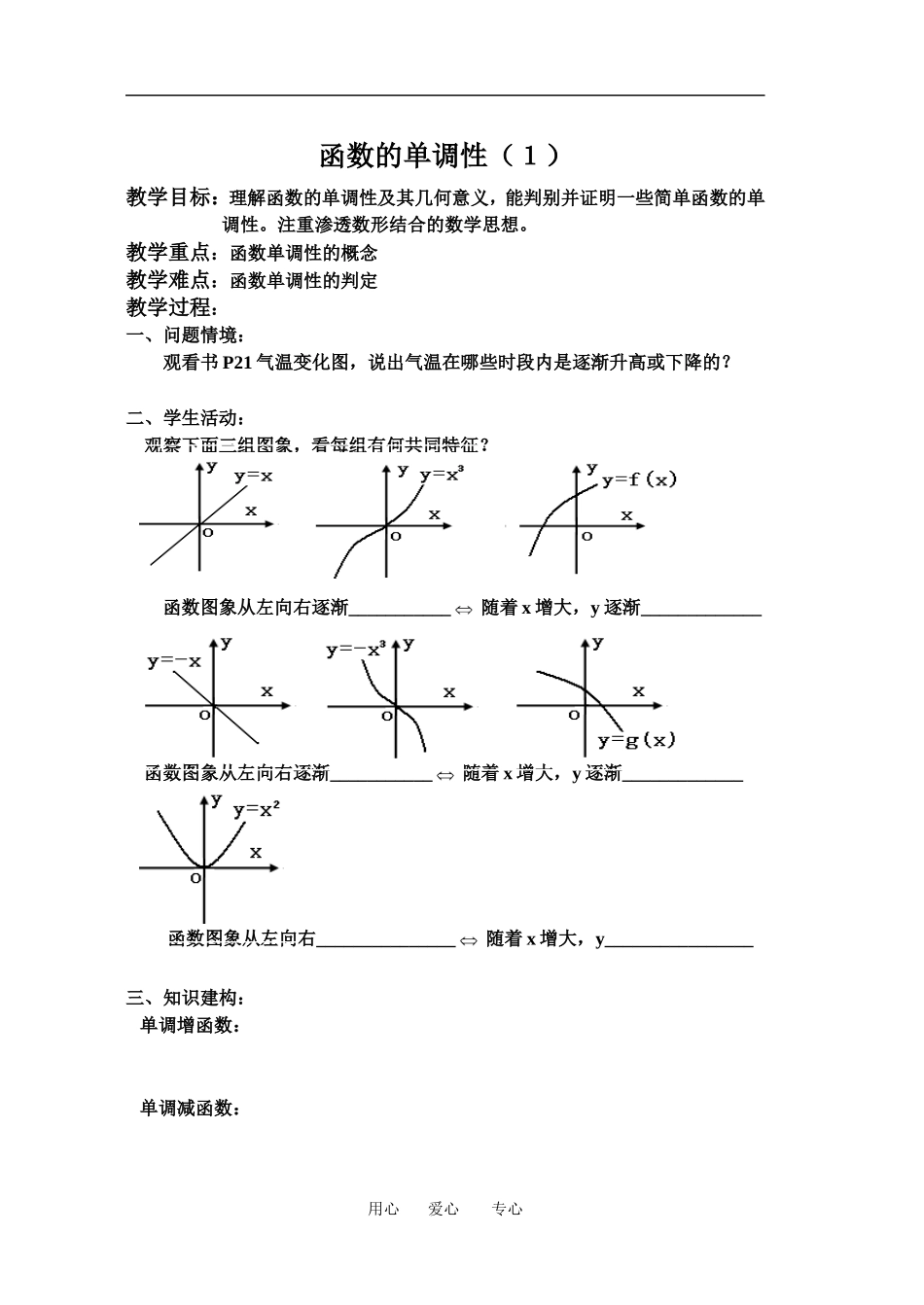
函数的单调性（１）教学目标：理解函数的单调性及其几何意义，能判别并证明一些简单函数的单调性。注重渗透数形结合的数学思想。教学重点：函数单调性的概念教学难点：函数单调性的判定 教学过程：一、问题情境：观看书 P21 气温变化图，说出气温在哪些时段内是逐渐升高或下降的？二、学生活动： 观察下面三组图象，看每组有何共同特征？函数图象从左向右逐渐___________随着 x 增大，y 逐渐_____________ 函数图象从左向右逐渐___________随着 x 增大，y 逐渐_____________ 函数图象从左向右_______________随着 x 增大，y________________ 三、知识建构： 单调增函数： 单调减函数：用心 爱心 专心四、知识运用：例 1、画出下列函数图象，并写出单调区间。 （1）y=x2+2 （2）y= （x≠0）小结：例 2、求证：函数 f（x）=1 在区间（∞，0）上是单调增函数。小结：练习：书 P37 1、2、6、7 五、回顾反思:知识: 思想方法:六、作业布置:书 P43 1、7（1）（2）（4）用心 爱心 专心函数的单调性（１）教学目标：理解函数的单调性及其几何意义，能判别并证明一些简单函数的单调性。注重渗透数形结合的数学思想。教学重点：函数单调性的概念教学难点：函数单调性的判定 教学过程：一、问题情境：观看书 P21 气温变化图，说出气温在哪些时段内是逐渐升高或下降的？二、学生活动： 观察下面三组图象，看每组有何共同特征？函数图象从左向右逐渐 上升 随着 x 增大，y 逐渐 变大 函数图象从左向右逐渐 下降 随着 x 增大，y 逐渐 变小 函数图象从左向右 有降有升 随着 x 增大，y 先变小再变大 思考：如何量化上述“上升”“下降”这一形的变化趋势？析：“从左向右”如何量化？沿 x 轴方向任取两实数 x1,x2，对应的函数值设为y1,y2，即点（x1,y1）,（x2,y2）在函数图象上，再沿 y 轴方向，你有何发现？用心 爱心 专心642-2-4-55（x2,y2）（x1,y1）g x  = x三、知识建构： 单调增函数： 单调减函数：四、知识运用：例 1、画出下列函数图象，并写出单调区间。 （1）y=x2+2 （2）y= （x≠0）解析：（1）642-2-4-55h x  = -x2+2增区间为（-∞，0），减区间为（0，+∞）（2）642-2-4-10-55q x  = 1x用心 爱心 专心减区间为（-∞，0），（0，+∞）小结：（1）图象法求函数单调区间；（2）单调区间宁开不闭（函数在某一点处不具有单调性，）；（3）几个单调区间之...