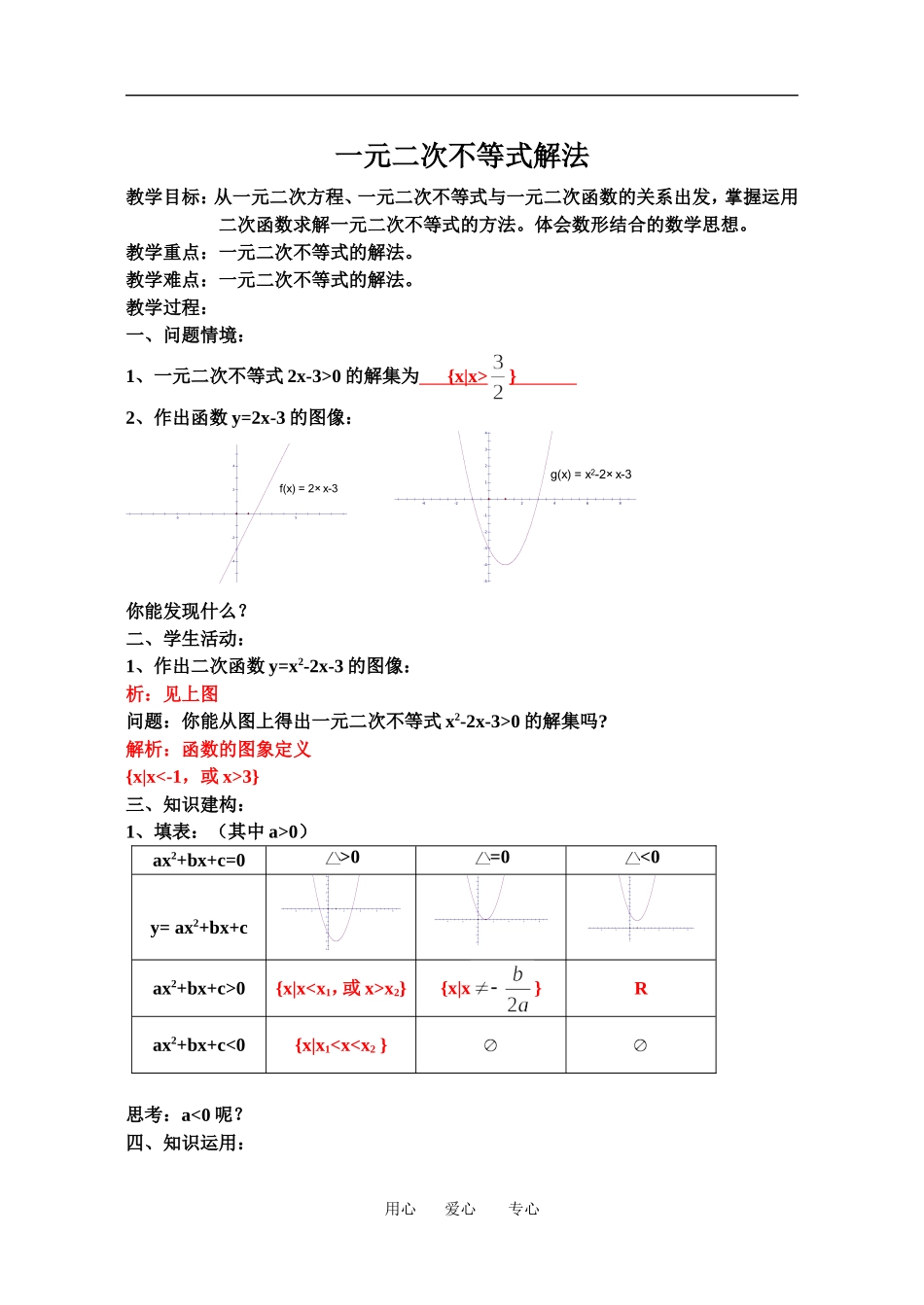
一元二次不等式解法教学目标:从一元二次方程、一元二次不等式与一元二次函数的关系出发,掌握运用二次函数求解一元二次不等式的方法。体会数形结合的数学思想。教学重点:一元二次不等式的解法。教学难点:一元二次不等式的解法。教学过程:一、问题情境:1、一元二次不等式 2x-3>0 的解集为_______________________.2、作出函数 y=2x-3 的图像:你能发现什么?二、学生活动:1、作出二次函数 y=x2-2x-3 的图像:问题:你能从图上得出一元二次不等式 x2-2x-3>0 的解集吗?三、知识建构:1、填表:(其中 a>0)ax2+bx+c=0>0=0<0y= ax2+bx+cax2+bx+c>0ax2+bx+c<0思考:a<0 呢?用心 爱心 专心四、知识运用:例 1、解不等式。 (1)x2-x-6>0 (2)-2x2-x+3≥0 (3)x2+x+2>0小结:例 2、解不等式。(1)x2-ax-2a2<0小结:练习:1、解下列不等式 (1)x2+3x-4≤0 (2)-x2-5x+3<0 (3)3x2-2x+3<0五、回顾反思:知识: 思想方法六、作业布置:用心 爱心 专心一元二次不等式解法教学目标:从一元二次方程、一元二次不等式与一元二次函数的关系出发,掌握运用二次函数求解一元二次不等式的方法。体会数形结合的数学思想。教学重点:一元二次不等式的解法。教学难点:一元二次不等式的解法。教学过程:一、问题情境:1、一元二次不等式 2x-3>0 的解集为 {x|x> } 2、作出函数 y=2x-3 的图像:42-2-4-55f x( ) = 2× x-3 4321-1-2-3-4-5-4-22468g x( ) = x2-2× x-3你能发现什么?二、学生活动:1、作出二次函数 y=x2-2x-3 的图像:析:见上图问题:你能从图上得出一元二次不等式 x2-2x-3>0 的解集吗?解析:函数的图象定义{x|x<-1,或 x>3}三、知识建构:1、填表:(其中 a>0)ax2+bx+c=0>0=0<0y= ax2+bx+c4321-1-2-3-4-5-4-2246854321-1-2-3-4-224687654321-1-4-22468ax2+bx+c>0{x|xx2}{x|x}Rax2+bx+c<0{x|x10 (2)-2x2-x+3≥0 (3)x2+x+2>0解析:(1)原不等式可化为(x-3)(x+2)>0,解得 x<-2,或 x>3∴原不等式解集为{x| x<-2,或 x>3}(2)原不等式可化为(x-1)(2x+3)≤0,解得∴原不等式解集为{x| }(3)其对应方程(x-3)(x+2)=0 的△<0,∴原不等式解集为 R小结:一看(二次项系数符号),二算(对应方程根)、三写(解集)例 2、解不等式。(2)x2-ax-2a2<0解析:原不等式可化为(x-2a)(x+a)<...