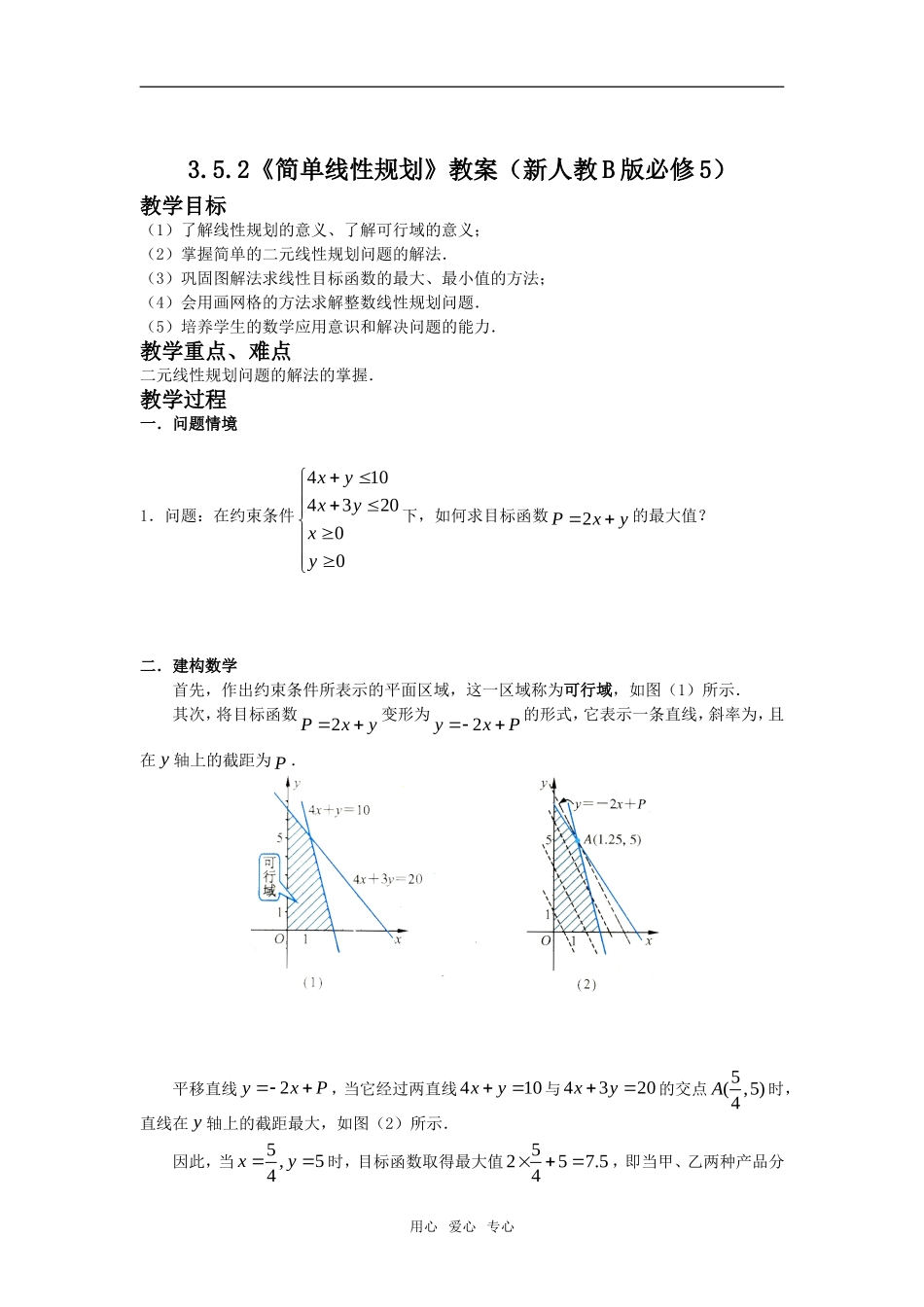
3.5.2《简单线性规划》教案(新人教 B 版必修 5)教学目标(1)了解线性规划的意义、了解可行域的意义;(2)掌握简单的二元线性规划问题的解法.(3)巩固图解法求线性目标函数的最大、最小值的方法;(4)会用画网格的方法求解整数线性规划问题.(5)培养学生的数学应用意识和解决问题的能力.教学重点、难点二元线性规划问题的解法的掌握.教学过程一.问题情境1.问题:在约束条件410432000xyxyxy 下,如何求目标函数2Pxy的最大值?二.建构数学首先,作出约束条件所表示的平面区域,这一区域称为可行域,如图(1)所示.其次,将目标函数2Pxy变形为2yxP的形式,它表示一条直线,斜率为,且在 y 轴上的截距为 P .平移直线2yxP,当它经过两直线410xy与4320xy的交点5( ,5)4A时,直线在 y 轴上的截距最大,如图(2)所示.因此,当5 ,54xy 时,目标函数取得最大值5257.54 ,即当甲、乙两种产品分用心 爱心 专心别生产 54 t 和5t 时,可获得最大利润7.5万元.这类求线性目标函数在线性约束条件下的最大值或最小值问题,通常称为线性规划问题.其中 5( ,5)4使目标函数取得最大值,它叫做这个问题的最优解.对于只含有两个变量的简单线性规划问题可用图解法来解决.说明:平移直线2yxP时,要始终保持直线经过可行域(即直线与可行域有公共点).三.数学运用例 1.设2zxy,式中变量 ,x y 满足条件4335251xyxyx ,求 z 的最大值和最小值.解:由题意,变量 ,x y 所满足的每个不等式都表示一个平面区域,不等式组则表示这些平面区域的公共区域.由图知,原点(0,0) 不在公共区域内,当0,0xy 时,20zxy ,即点 (0,0) 在直线0l :20xy 上,作一组平行于0l 的直线l :2xyt ,tR,可知:当l 在0l 的右上方时,直线l 上的点( , )x y满足20xy ,即0t ,而且,直线l 往右平移时,t 随之增大.由图象可知,当直线l 经过点(5,2)A时,对应的t 最大,当直线l 经过点(1,1)B时,对应的t 最小,所以,max2 5212z ,min2 1 13z .例 2.设610zxy,式中 ,x y 满足条件4335251xyxyx ,求 z 的最大值和最小值.用心 爱心 专心OyxACB43 0xy 1x 3525 0xy解:由引例可知:直线0l 与 AC 所...