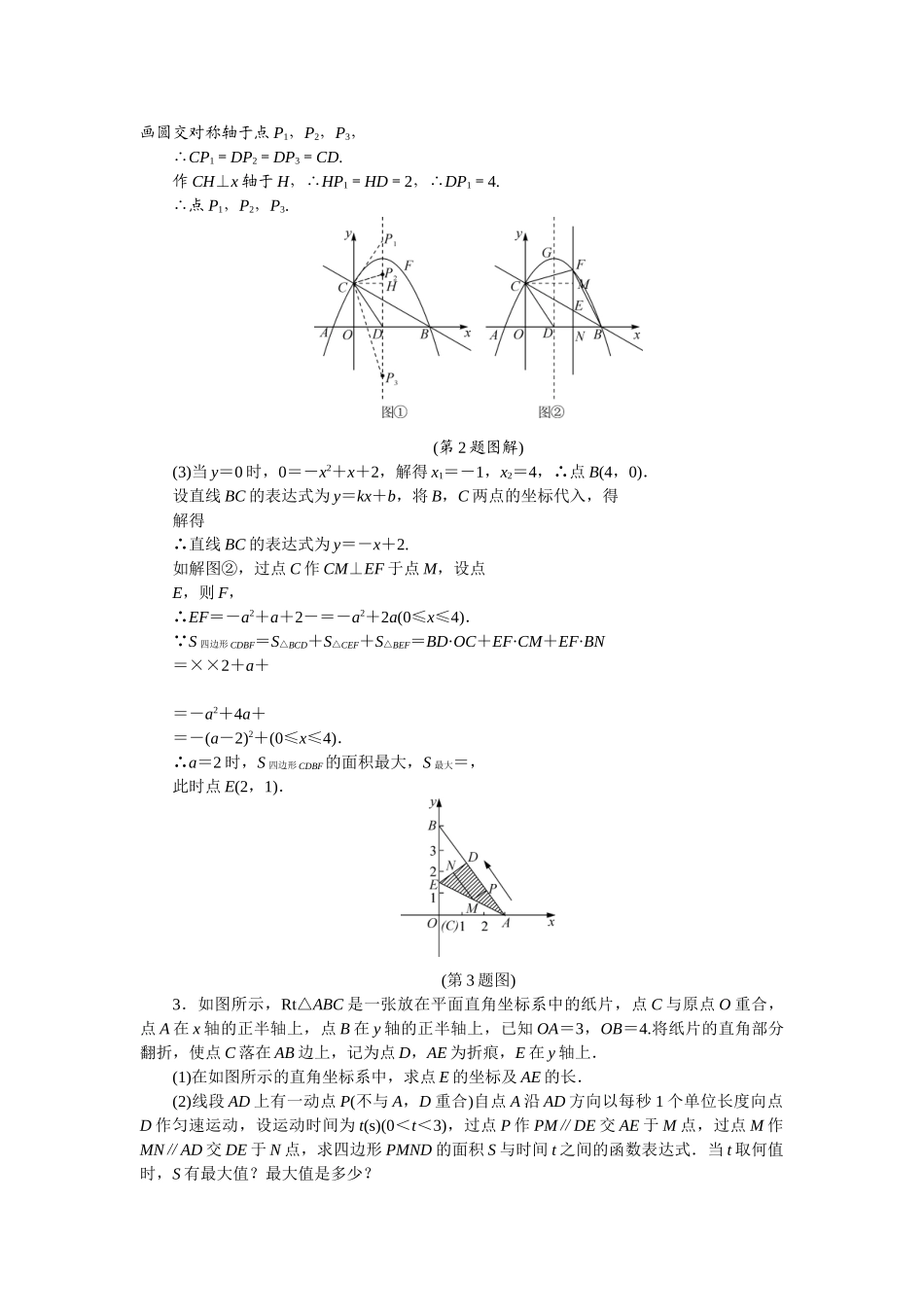
2024 年海南省海口九年级数学综合性压轴题(第 1 题图)1.如图,抛物线 y=x2+bx+c 与 y 轴交于点 C(0,-4),与 x 轴交于点 A,B,且 B 点的坐标为(2,0).(1)求该抛物线的表达式.(2)若点 P 是 AB 上的一动点,过点 P 作 PE∥AC,交 BC 于 E,连结 CP,求△PCE 面积的最大值.(3)若点 D 为 OA 的中点,点 M 是线段 AC 上一点,且△OMD 为等腰三角形,求 M 点的坐标.解:(1)把点 C(0,-4),B(2,0)的坐标分别代入 y=x2+bx+c 中,得解得∴该抛物线的表达式为 y=x2+x-4.(2)令 y=0,即 x2+x-4=0,解得 x1=-4,x2=2,∴点 A(-4,0),S△ABC=AB·OC=12.设点 P 的坐标为(x,0),则 PB=2-x. PE∥AC,∴∠BPE=∠BAC,∠BEP=∠BCA,∴△PBE∽△ABC.∴=()2,即=()2,化简,得 S△PBE=(2-x)2.S△PCE=S△PCB-S△PBE=PB·OC-S△PBE=·(2-x)·4-(2-x)2=-x2-x+=-(x+1)2+3,∴当 x=-1 时,S△PCE的最大值为 3.(3)△OMD 为等腰三角形,可能有三种情形:(Ⅰ)当 DM=DO 时,如解图①所示.DO=DM=DA=2,∴∠OAC=∠AMD=45°,∴∠ADM=90°,∴点 M 的坐标为(-2,-2). ,(第 1 题图解))(Ⅱ)当 MD=MO 时,如解图②所示.过点 M 作 MN⊥OD 于点 N,则点 N 为 OD 的中点,∴DN=ON=1,AN=AD+DN=3,又 △AMN 为等腰直角三角形,∴MN=AN=3,∴点 M 的坐标为(-1,-3).(Ⅲ)当 OD=OM 时, △OAC 为等腰直角三角形,∴点 O 到 AC 的距离为×4=2,即 AC 上的点与点 O 之间的最小距离为 2. 2>2,∴OD=OM 的情况不存在.综上所述,点 M 的坐标为(-2,-2)或(-1,-3).(第 2 题图)2.如图,抛物线 y=-x2+mx+n 与 x 轴交于 A,B 两点,与 y 轴交于点 C,抛物线的对称轴交 x 轴于点 D,已知点 A(-1,0),C(0,2).(1)求抛物线的表达式.(2)在抛物线的对称轴上是否存在点 P,使△PCD 是以 CD 为腰的等腰三角形?假如存在,直接写出点 P 的坐标;假如不存在,请说明理由.(3)点 E 时线段 BC 上的一个动点,过点 E 作 x 轴的垂线与抛物线交于点 F,当点 E 运动到什么位置时,四边形 CDBF 的面积最大?求出四边形 CDBF 的最大面积及此时点 E 的坐标.解:(1) 抛物线 y=-x2+mx+n 经过点 A(-1,0),C(0,2),∴解得∴抛物线的表达式为 y=-x2+x+2.(2) y=-x...