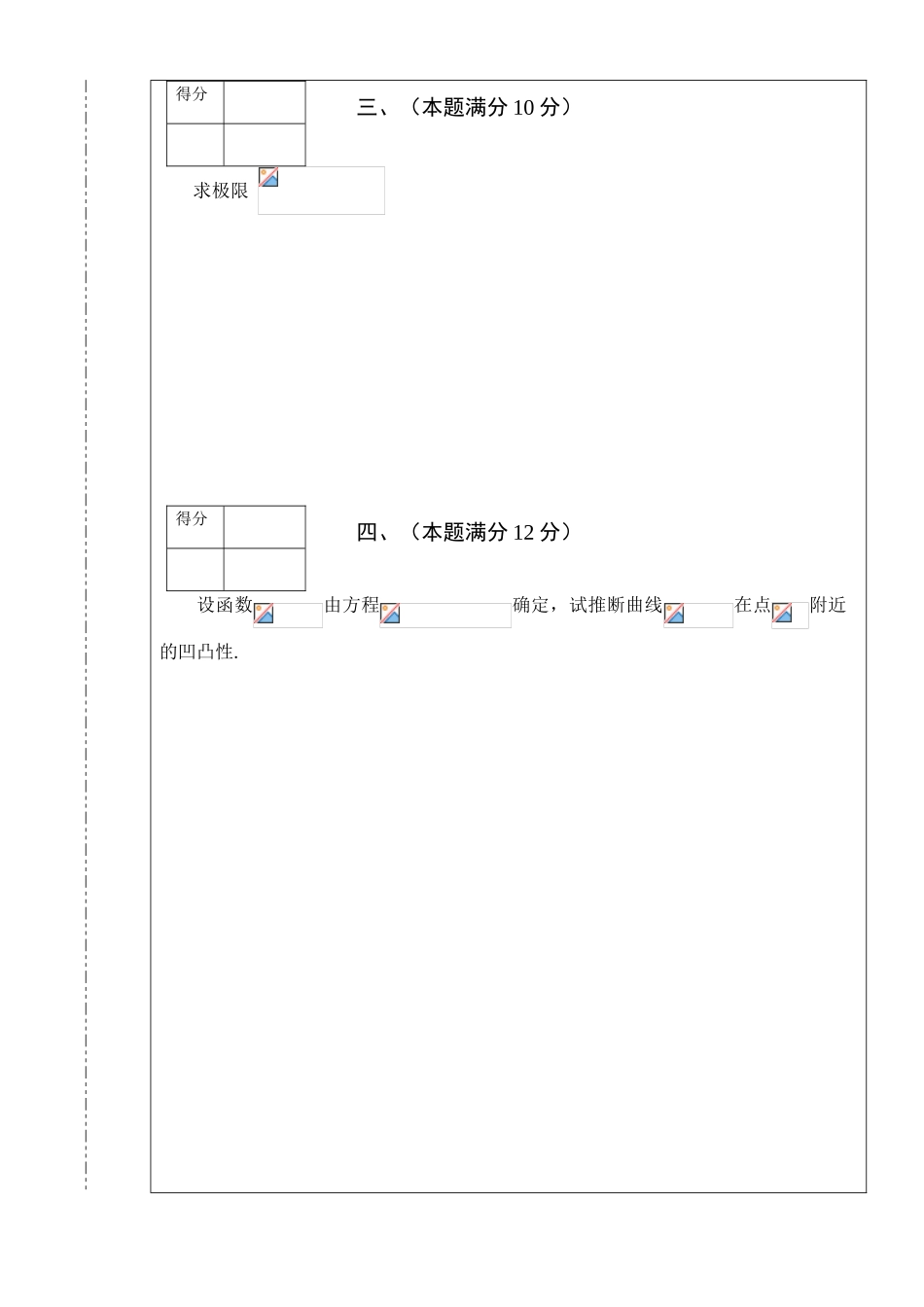
南昌大学第四届高等数学竞赛(文科类)试题得分1.设时,与是同阶无穷小,则正整数为 . 1 2 3 序号 姓名 学院 专业 学号 考试日期: 2024.9.16 题号一二三四五六七八九十总分累分人签名题分1515101212121212100得分考生注意事项:1.本试卷共 6 页,请查看试卷中是否有缺页或破损,如有立即举手报告以便更换.2.考试结束后,考生不得将试卷、答题纸和草稿纸带出考场.得分评阅人 1. . 2.设,则= .3.设,则 .4. . 5.设连续,则 . 一、填空题(本题共 5 小题,每小题 3 分,满分 15分.把答案填在题中横线上)二、选择题(本题共 5 小题,每小题 3 分,满分 15 分.每小题给出的四个选项中只有一项符合题目的要求,把所选项前的字母填在题后的括号内)得分 求极限 得分 设函数由方程确定,试推断曲线在点附近的凹凸性. 三、(本题满分 10 分)四、(本题满分 12 分)得分评阅人 设,求不定积分得分 设是函数在区间上使用 Lagrange(拉格朗日)中值定理中的“中值”,求极限.五、(本题满分 12 分)六、(本题满分 12 分)得分评阅人 求曲线的一条切线,使得该曲线与切线 及直线和所围成的图形绕轴旋转的旋转体的体积为最小.七、(本题满分 12 分)得分评阅人 设在区间上可微,且满足条件.试证:存在,使.八、(本题满分 12 分)