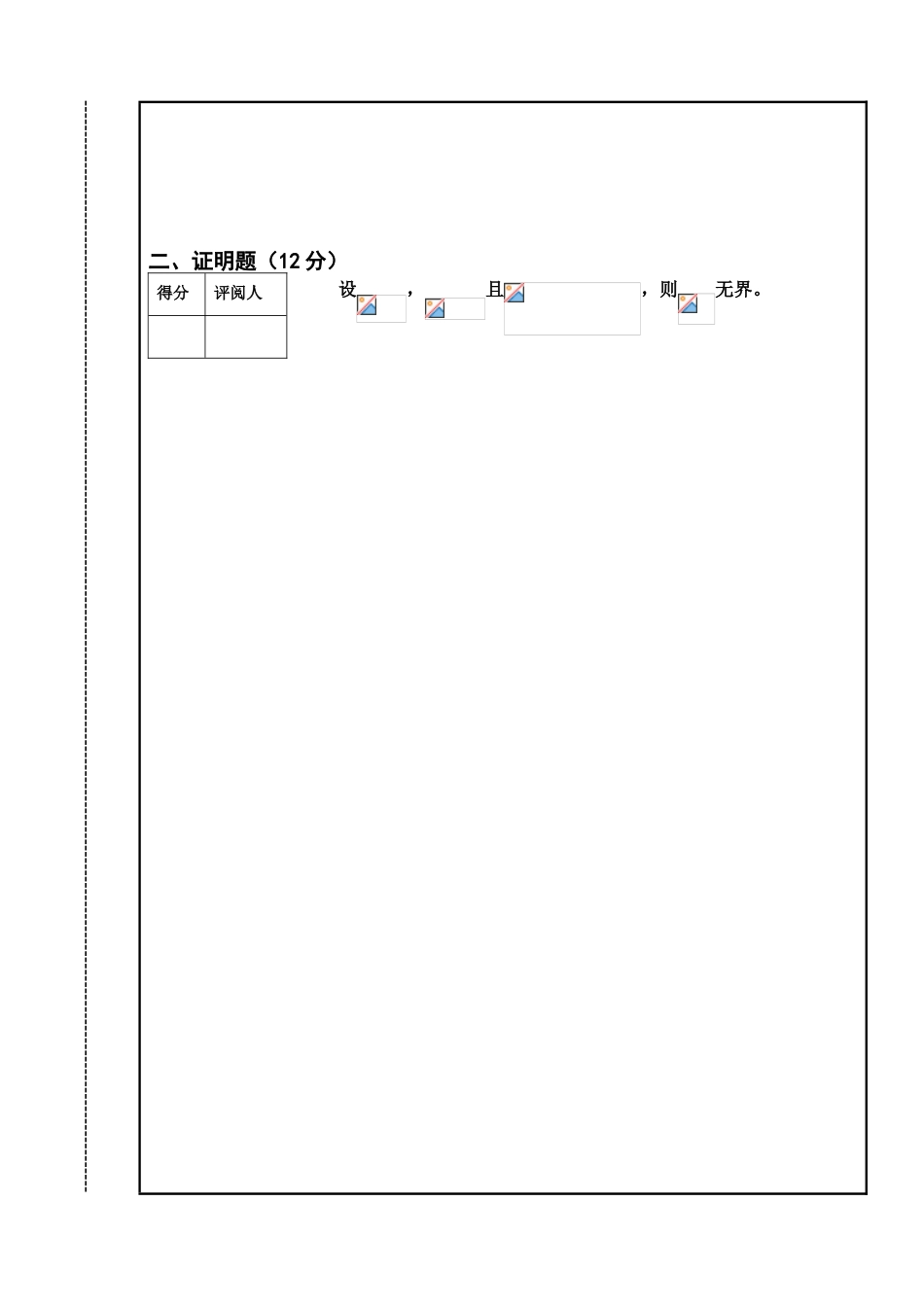
南昌大学第三届高等数学竞赛(数学专业类 2024、2024 级)试卷试卷编号: ( )卷课程名称: 适用班级: 姓名: 学号: 班级: 专业: 学院: 系别: 考试日期: 题号一二三四五六七八九十总分累 分 人 签名题分251213127724 100得分考生注意事项:1、本试卷共 9 页,请查看试卷中是否有缺页或破损。如有立即举手报告以便更换。 2、考试结束后,考生不得将试卷、答题纸和草稿纸带出考场。一、推断题(每题 5 分,共 25 分) 以下命题是正确的,请给以证明;不正确的,请举例说明。1、将数列分成无穷多个序列:,,…,,…。它们均收敛于同一个极限,则必收敛。这里,。2、设函数在可导,则在的某个邻域内连续。3、设在内有定义,若对任意正数,有,则存在(极限有限)。4、若函数序列在区间上内闭一致收敛,则它在上收敛。5、。得分评阅人 二、证明题(12 分)设,且,则无界。得分评阅人 三、证明题(13 分) 设,,则(i)在一致连续;(ii)在不一致连续。得分评阅人 四、证明题(12 分) 设 函 数在上 有 二 阶 导 数 ,,,则存在,使得。得分评阅人 五、证明题(7 分)设,分 别 在 区 间,上 连 续 , 定 义。按定义证明在矩形域内可微。得分评阅人 六、证明题(7 分) 计算,其中是以,,,为顶点的矩形边界,积分沿的正向计算。得分评阅人 七、证明题(24 分) 给函数项级数。得分评阅人 (i)求此级数的收敛域;(ii)证明此级数在上一致收敛; (iii)证明此级数在不一致收敛; (iv)证明此级数在内处处连续; (v)求。 (vi)在内,。