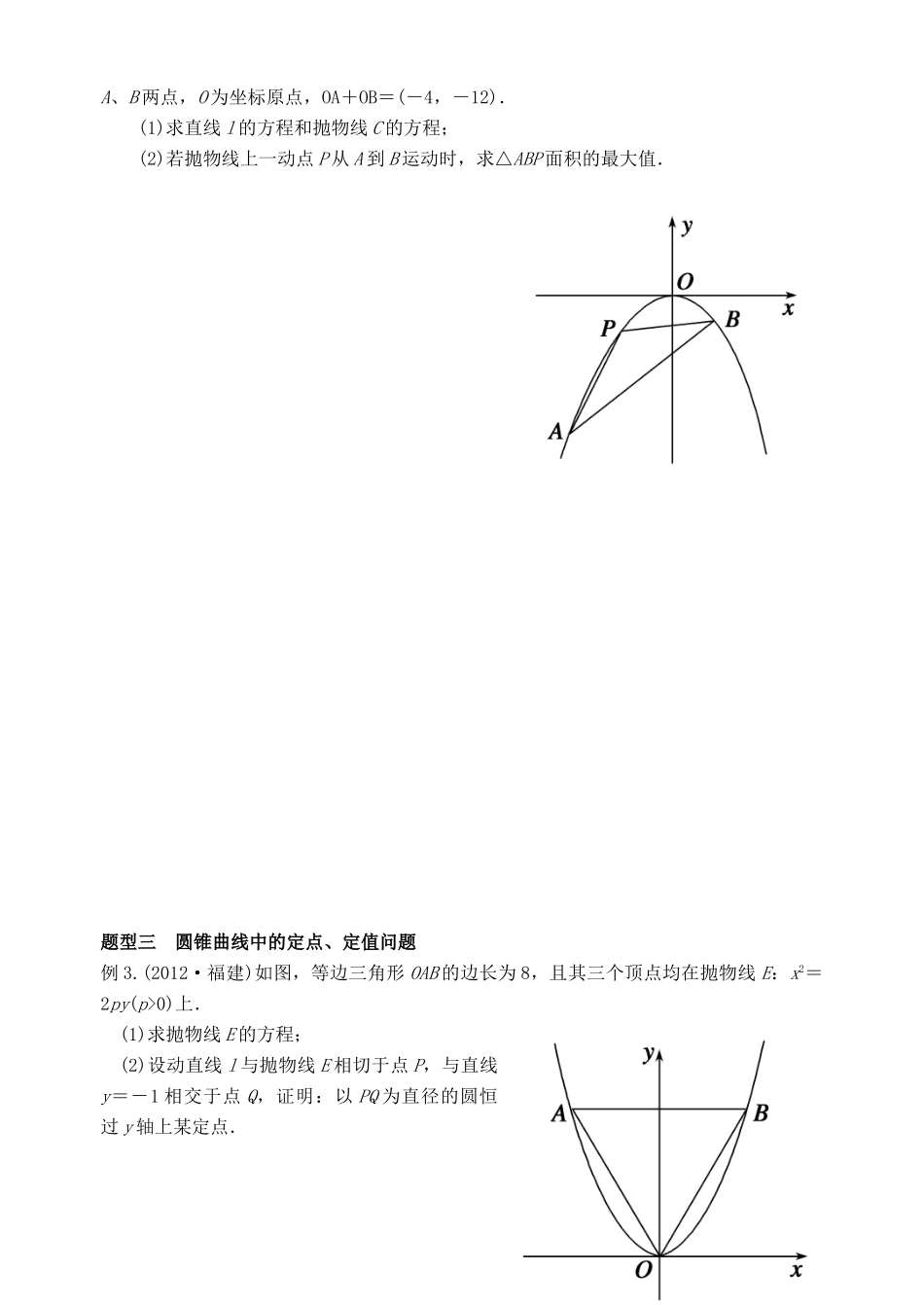
山东省高密市第三中学高三数学 8.9 直线与圆锥曲线的位置关系复习导学案一、基础梳理:1.直线 ∶Ax+B+C=0 与椭圆 C∶f(x,y)=0 的位置关系可分为:相交、相切、相离.2.三种位置关系的判定条件:设直线 :Ax+By+C=0, 椭圆 C:f(x,y)=0,由消去 y(或消去 x)得:ax2+bx+c=0,△=b2-4ac,△>0相交 △<0相离 △= 0相切3.直线与椭圆相交的弦长公式若直线与椭圆交于两点,★ 弦长: =.二、课内探究:题型一 求参数的取值范围例 1. 在直角坐标平面内,已知点, 是平面内一动点,直线、斜率之积为. (Ⅰ)求动点的轨迹的方程;(Ⅱ)过点作直线 与轨迹交于两点,线段的中点为,求直线的斜率的取值范围.跟踪训练 1:如图所示,已知圆定点 A(1,0) , M 为圆上一动点,点 P 在 AM 上,点 N 在 CM 上,且满足,点 N 的轨迹为曲线 E.(1)求曲线 E 的方程;(2)若过定点 F(0,2)的直线交曲线 E 于不同的两点 G、H(点 G 在点 F、H 之间),且满足的取值范围.题型二 圆锥曲线中的范围、最值问题例 2.如图,已知直线 l:y=kx-2 与抛物线 C:x2=-2py(p>0)交于A、B 两点,O 为坐标原点,OA+OB=(-4,-12).(1)求直线 l 的方程和抛物线 C 的方程;(2)若抛物线上一动点 P 从 A 到 B 运动时,求△ABP 面积的最大值.题型三 圆锥曲线中的定点、定值问题例 3.(2012·福建)如图,等边三角形 OAB 的边长为 8,且其三个顶点均在抛物线 E:x2=2py(p>0)上.(1)求抛物线 E 的方程;(2)设动直线 l 与抛物线 E 相切于点 P,与直线y=-1 相交于点 Q,证明:以 PQ 为直径的圆恒过 y 轴上某定点.题型四 圆锥曲线中的探索性问题例 4.已知中心在原点的椭圆 C:+=1 的一个焦点为 F1(0,3),M(x,4)(x>0)为椭圆 C 上一点,△MOF1的面积为.(1)求椭圆 C 的方程;(2)是否存在平行于 OM 的直线 l,使得直线 l 与椭圆 C 相交于 A,B 两点,且以线段 AB为直径的圆恰好经过原点?若存在,求出直线 l 的方程;若不存在,说明理由.题型五 直线、圆及圆锥曲线的交汇问题例 5.(2013·浙江)如图,点 P(0,-1)是椭圆 C1:+=1(a>b>0) 的一个顶点,C1的长轴是圆 C2:x2+y2=4 的直径.l1,l2 是过点 P 且互相垂直的两条直线,其中 l1 交圆 C2 于A,B 两点,l2交椭圆 C1于另一点 D.(1)求椭圆 C1的方程;(2)求△ABD 面积取最大值时直线 l1的方程.直线与...