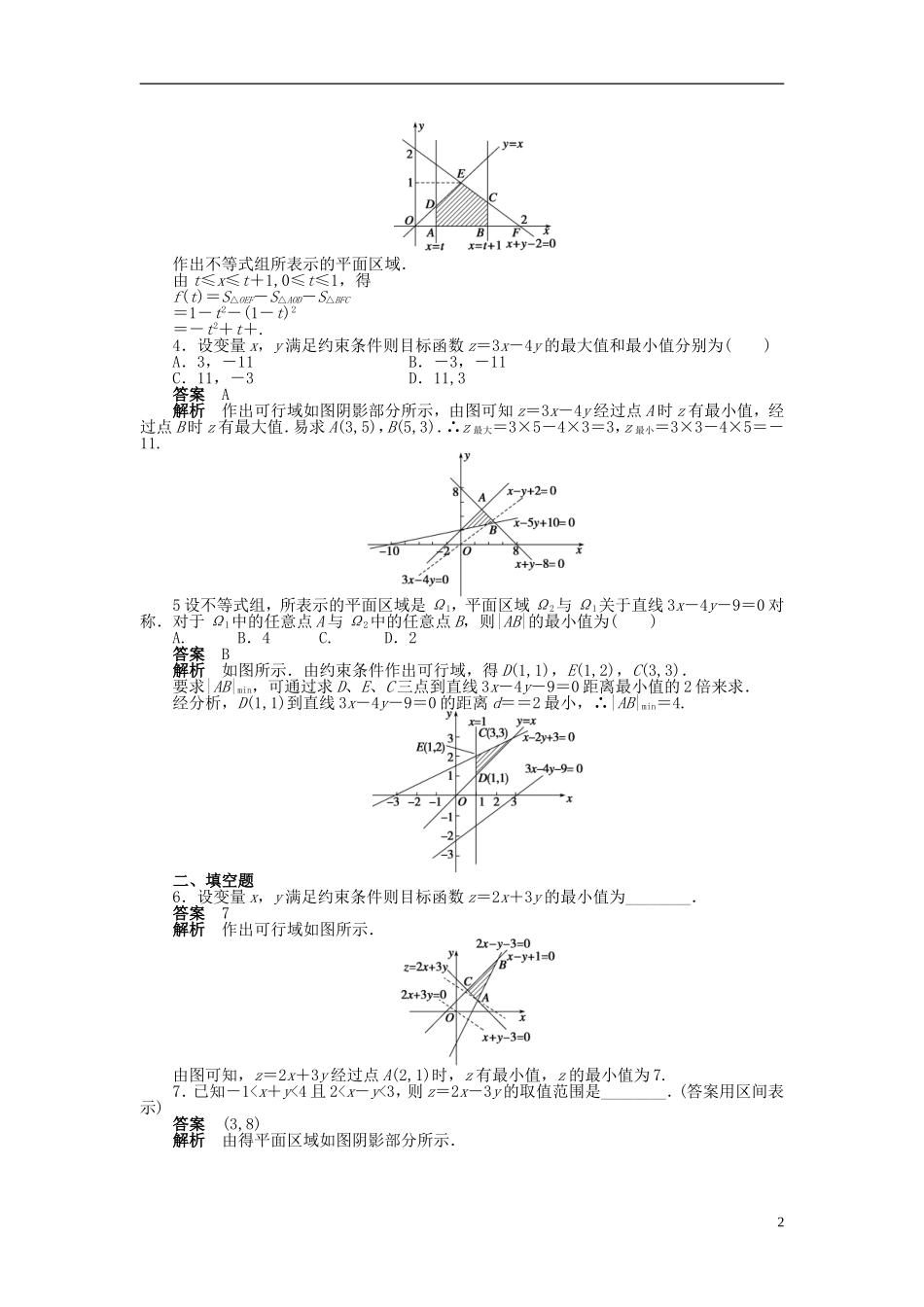
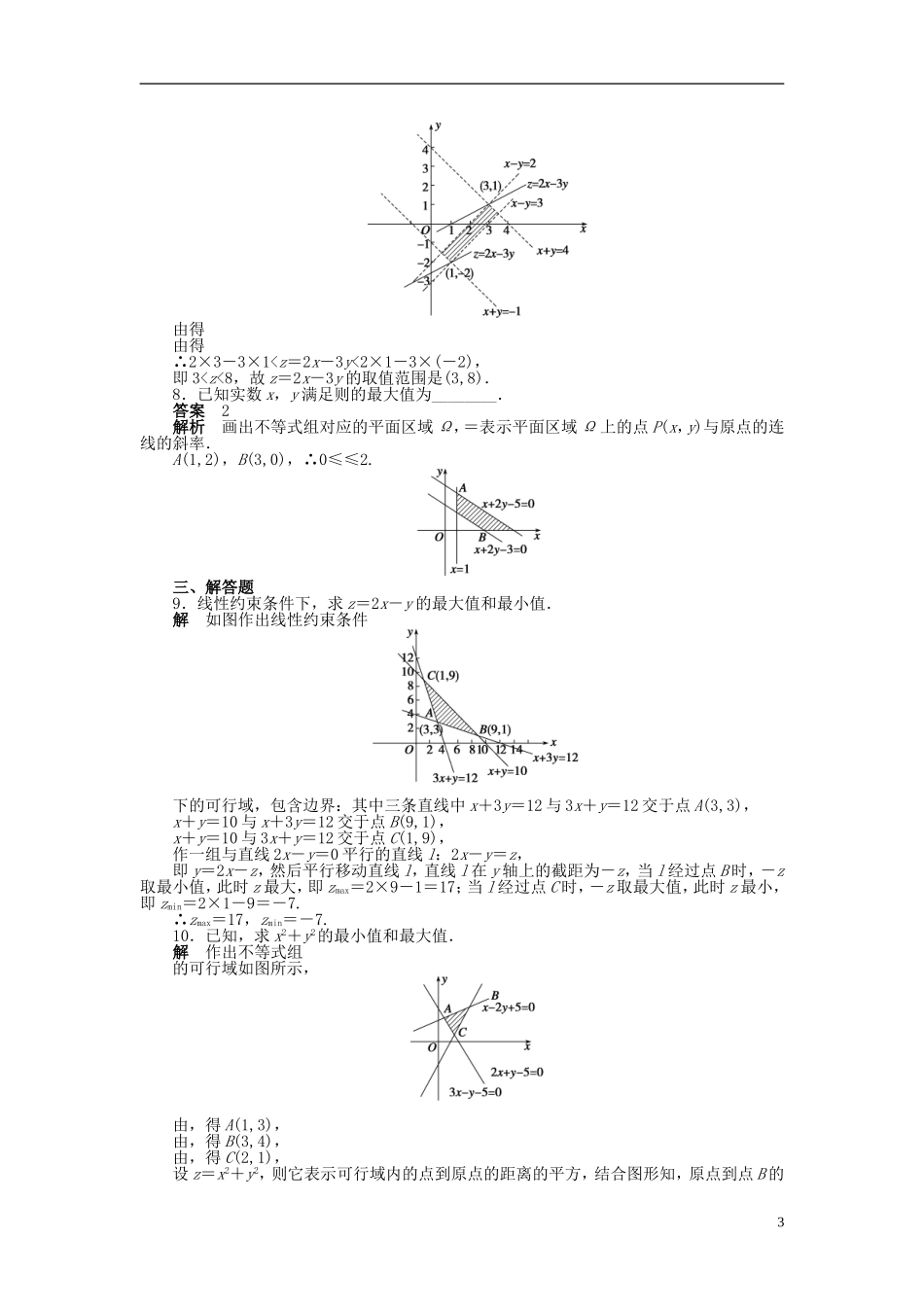
3.3.2 简单的线性规划问题(一)课时目标1.了解线性规划的意义.2.会求一些简单的线性规划问题.线性规划中的基本概念名称意义约束条件由变量 x,y 组成的不等式或方程线性约束条件由 x,y 的一次不等式(或方程)组成的不等式组目标函数欲求最大值或最小值所涉及的变量 x,y 的函数解析式线性目标函数关于 x,y 的一次解析式可行解满足线性约束条件的解(x,y)可行域所有可行解组成的集合最优解使目标函数取得最大值或最小值的可行解线性规划问题在线性约束条件下求线性目标函数的最大值或最小值问题一、选择题 1.若实数 x,y 满足不等式组则 x+y 的最大值为( )A.9 B. C.1 D.答案 A解析 画出可行域如图:当直线 y=-x+z 过点 A 时,z 最大.由得 A(4,5),∴zmax=4+5=9.2.已知点 P(x,y)的坐标满足条件则 x2+y2的最大值为( )A. B.8 C.16 D.10答案 D解析 画出不等式组对应的可行域如下图所示:易得 A(1,1),|OA|=,B(2,2),|OB|=2,C(1,3),|OC|=.∴(x2+y2)max=|OC|2=()2=10.3.在坐标平面上有两个区域 M 和 N,其中区域 M=,区域 N={(x,y)|t≤x≤t+1,0≤t≤1},区域 M 和 N 公共部分的面积用函数 f(t)表示,则 f(t)的表达式为( )A.-t2+t+ B.-2t2+2tC.1-t2 D.(t-2)2答案 A解析 1作出不等式组所表示的平面区域.由 t≤x≤t+1,0≤t≤1,得f(t)=S△OEF-S△AOD-S△BFC=1-t2-(1-t)2=-t2+t+.4.设变量 x,y 满足约束条件则目标函数 z=3x-4y 的最大值和最小值分别为( )A.3,-11 B.-3,-11C.11,-3 D.11,3答案 A解析 作出可行域如图阴影部分所示,由图可知 z=3x-4y 经过点 A 时 z 有最小值,经过点 B 时 z 有最大值.易求 A(3,5),B(5,3).∴z 最大=3×5-4×3=3,z 最小=3×3-4×5=-11.5 设不等式组,所表示的平面区域是 Ω1,平面区域 Ω2与 Ω1关于直线 3x-4y-9=0 对称.对于 Ω1中的任意点 A 与 Ω2中的任意点 B,则|AB|的最小值为( )A. B.4 C. D.2答案 B解析 如图所示.由约束条件作出可行域,得 D(1,1),E(1,2),C(3,3).要求|AB|min,可通过求 D、E、C 三点到直线 3x-4y-9=0 距离最小值的 2 倍来求.经分析,D(1,1)到直线 3x-4y-9=0 的距离 d==2 最小,∴|AB|min=4.二、填空题6.设变量 x,y 满足约束条件则目标函数 z=2x+3y 的最小值为________.答案...