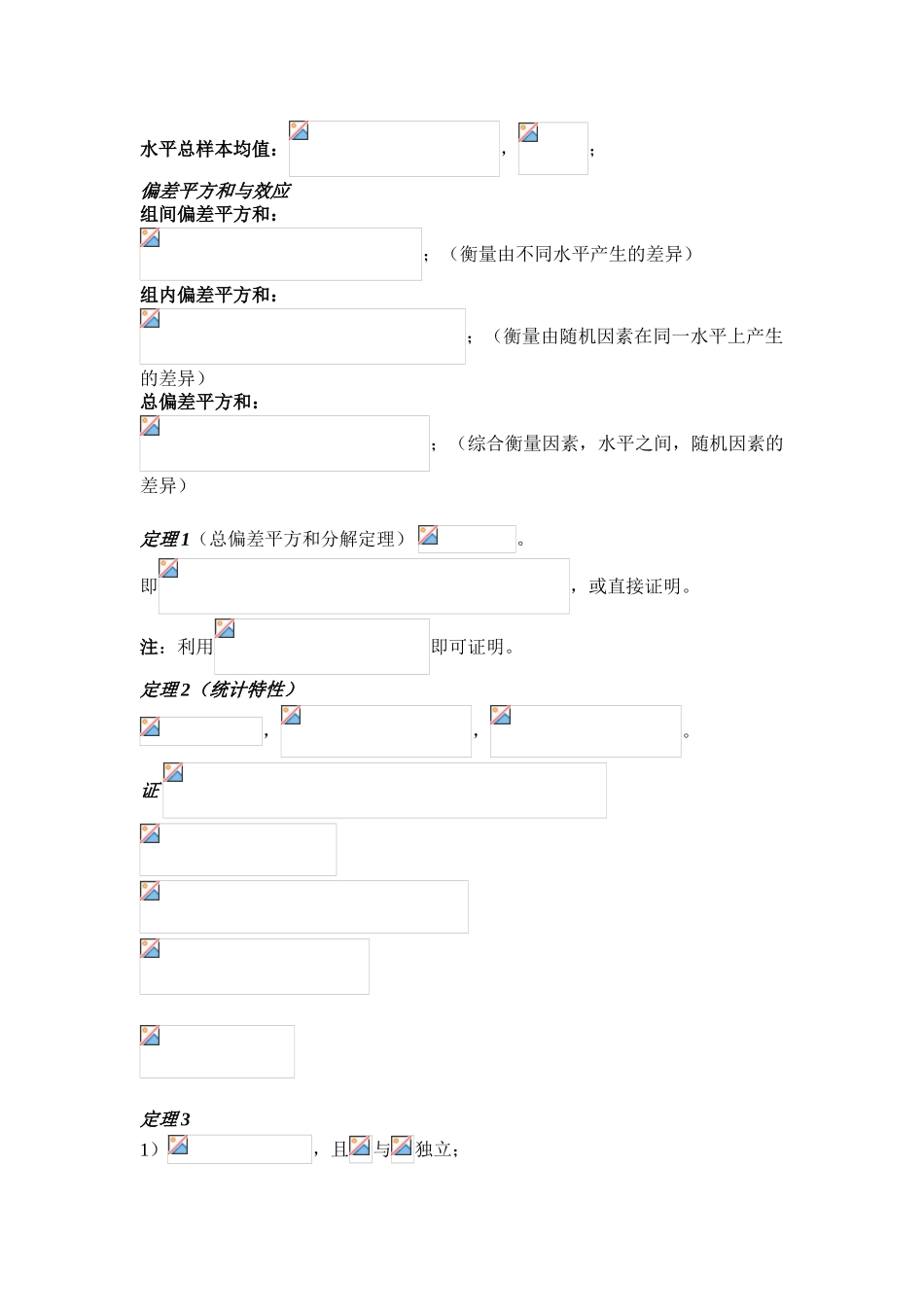
第八章 方差分析与回归分析§1 单因素试验的方差分析试验指标:讨论对象的某种特征。例 各人的收入。因素:与试验指标相关的条件。例 各人的学历,专业,工作经历等与工资有关的特征。因素水平:因素所在的状态例 学历是因素,而高中,大学,讨论生等,就是学历因素水平;数学,物理等就是专业的水平。问题:各因素水平对试验指标有无显著的差异?单因素试验方差分析模型假设1) 影响试验指标的因素只有一个,为,其水平有 个:;2) 每个水平下,试验指标是一个总体。各个总体的抽样过程是独立的。3),且。问题:分析水平对指标的影响是否相同1)对每个总体抽样得到样本,由其检验假设:原假设,;备选假设:,;2)假如拒绝原假设,则对未知参数进行参数估量。注1)接受假设即认为:各个水平之间没有显著差异,反之则有显著差异。2)在水平只有两个时,问题就是双正态总体的均值假设检验问题和参数估量问题。检验方法数 据 结 构 式 :, 偏 差是 相 互 独 立 的 ,。不难验证,。各类样本均值水平的样本均值:;水平总样本均值:,;偏差平方和与效应组间偏差平方和:;(衡量由不同水平产生的差异)组内偏差平方和:;(衡量由随机因素在同一水平上产生的差异)总偏差平方和:;(综合衡量因素,水平之间,随机因素的差异)定理 1(总偏差平方和分解定理) 。即,或直接证明。注:利用即可证明。定理 2(统计特性),,。证 定理 31),且与独立;2)假如假设成立,那么,;且假如假设,,则还有,。证 1)由于不同水平的样本间的独立性,较易处理。对固定的 ,,,且独立,所以由第五章定理 2 的结论,,利用可加性,即得,且与独立。注意到,因此也与独立,从而也与独立。注 这里只需方差假设相同,不需要假设均值相同。2),且独立,同样利用第五章定理 2,。但在假设成立时,,即得结论。且与独立。同时,。注 此处结论证明利用了都相等,即利用:。但上述结论在组样本容量不同时,直接利用正交变换仍可类似证明。 从统计角度看,假如假设成立,那么,而在假设不 成 立 时 ,, 即 统 计 量将有偏大的趋势。那么,大到何值可以采信为推翻假设的反例,就回到前面的假设检验问题了。定理 置信度为时,假设的检验问题的拒绝域为。参数估量问题假如各因素有显著差异,即对某些水平,那么就需要估量这些参数的值和。1.最大似然估量总体,密度函数为,所以最大似然函数为,一般,我们把分成两部分...