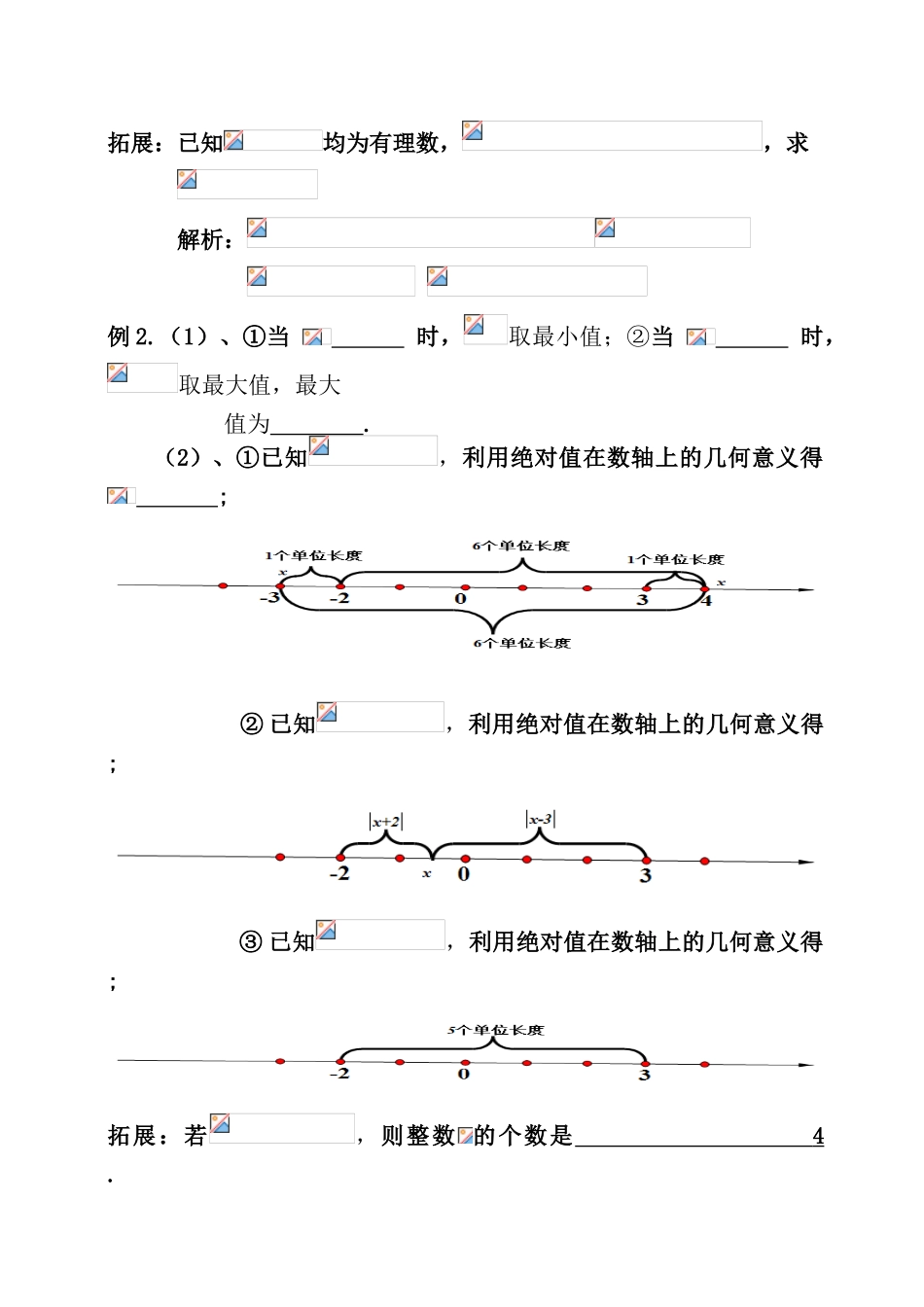
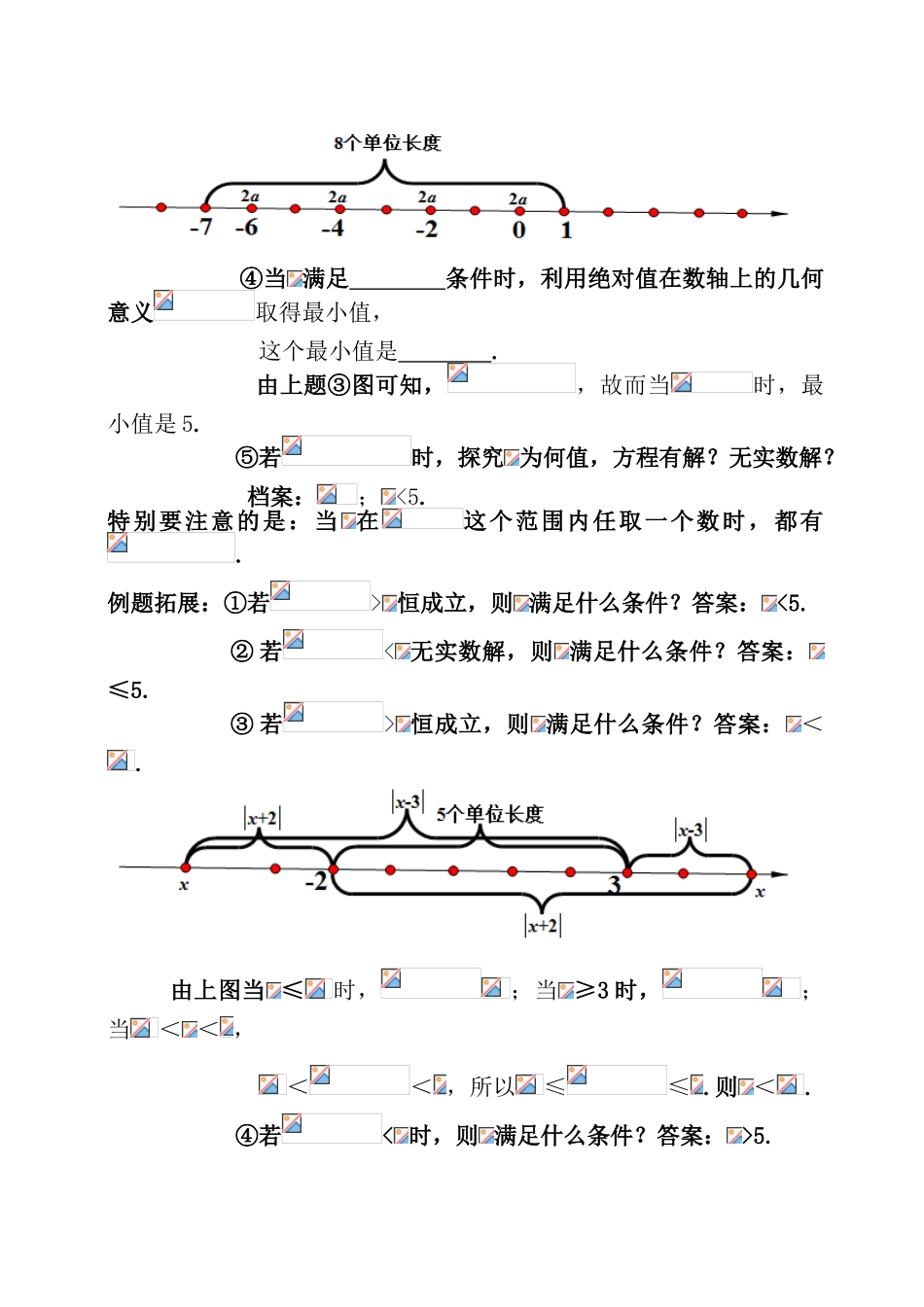
绝对值几何意义应用一、几何意义类型:类型一、:表示数轴上的点 到原点 0 的距离;类型二、 :表示数轴上的点 到点 的距离(或点 到点 的距离);类型三、:表示数轴上的点 到点的距离(点到点的距离);类型四、:表示数轴上的点 到点 的距离;类型五、:表示数轴上的点 到点的距离.二、例题应用:例 1.(1)、的几何意义是数轴上表示 的点与表示 的点之间的距离,若=2,则 .(2)、的几何意义是数轴上表示 的点与表示 的点之间的距离,若,则 .(3)、如图所示数轴上四个点的位置关系,且它们表示的数分别为 m、n、p、q.若, , 则 ; 若, 则 . (4)、不相等的有理数在数轴上的对应点为 A,B,C,假如, 则 点 A , B , C 在 数 轴 上 的 位 置 关 系 .拓展:已知均为有理数,,求 解析: 例 2.(1)、①当 时,取最小值;②当 时,取最大值,最大 值为 .(2)、①已知,利用绝对值在数轴上的几何意义得 ; ② 已知,利用绝对值在数轴上的几何意义得 ; ③ 已知,利用绝对值在数轴上的几何意义得 ; 拓展:若,则整数 的个数是 4 . ④当 满足 条件时,利用绝对值在数轴上的几何意义取得最小值, 这个最小值是 . 由上题③图可知,,故而当时,最小值是 5. ⑤若时,探究 为何值,方程有解?无实数解? 档案:; <5.特别要注意的是:当 在这个范围内任取一个数时,都有.例题拓展:①若> 恒成立,则 满足什么条件?答案: <5. ② 若< 无实数解,则 满足什么条件?答案:≤5. ③ 若> 恒成立,则 满足什么条件?答案: <. 由上图当 ≤时,;当 ≥3 时,;当< < , << ,所以≤≤ .则 <. ④若< 时,则 满足什么条件?答案: >5.拓展应用:已知,求的最大值和最小值. 解析:,, , ,, . (3)、当 满足 条件时,取最小值,这个最小值是 .由 以 上 图 形 可 知 : 当= 1 时 ,, 其 他 范 围 内﹥5,故而,这个最小值是 5 .(4)、当 满足 条件时,取最小值,这个最小值是 .由以上图形可知:当 时,,其他范围内﹥11,故而,这个最小值是 11 .特别要注意的是:当在这个范围内任取一个数时,都有.(5)、当 满足 条件时,取最小值, 这个最小值是 . 由以上图形可知:当 = 3 时,,其他范围内﹥13,故而,这个最小值是 13 .(6)、当 满足 条件时,取最小值, 这个最小值是 . 由以上图形可...