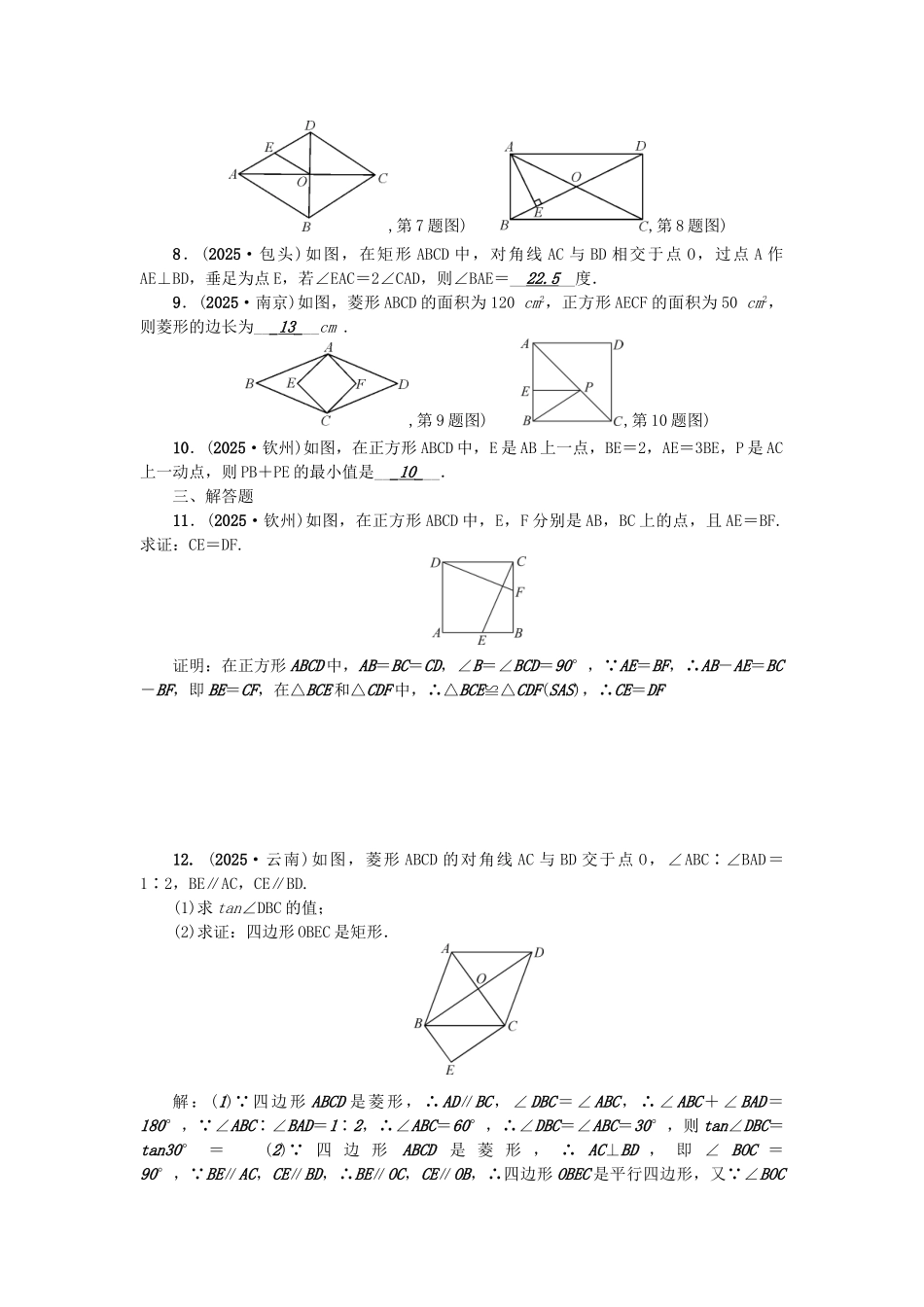
考点跟踪突破 19 矩形、菱形与正方形一、选择题1.(2025·无锡)下列性质中,菱形具有而矩形不一定具有的是( C )A.对角线相等 B.对角线互相平分C.对角线互相垂直 D.邻边互相垂直2.(2025·桂林)如图,在菱形 ABCD 中,AB=6,∠ABD=30°,则菱形 ABCD 的面积是( B )A.18 B.18 C.36 D.36,第 2 题图) ,第 3 题图)3.(2025·钦州)如图,要使▱ABCD 成为菱形,则需添加的一个条件是( B )A.AC=AD B.BA=BCC.∠ABC=90° D.AC=BD4.(2025·宁夏)菱形 ABCD 的对角线 AC,BD 相交于点 O,E,F 分别是 AD,CD 边上的中点,连接 EF,若 EF=,BD=2,则菱形 ABCD 的面积为( A )A.2 B. C.6 D.8,第 4 题图) ,第 5 题图)5.(2025·荆门)如图,在矩形 ABCD 中(AD>AB),点 E 是 BC 上一点,且 DE=DA,AF⊥DE,垂足为点 F,在下列结论中,不一定正确的是( B )A.△AFD≌△DCE B.AF=ADC.AB=AF D.BE=AD-DF6.(2025·宜宾)如图,点 P 是矩形 ABCD 的边 AD 上的一动点,矩形的两条边 AB,BC的长分别是 6 和 8,则点 P 到矩形的两条对角线 AC 和 BD 的距离之和是( A )A.4.8B.5C.6D.7.2二、填空题7.(2025·扬州)如图,菱形 ABCD 的对角线 AC,BD 相交于点 O,E 为 AD 的中点,若 OE=3,则菱形 ABCD 的周长为__24__.,第 7 题图) ,第 8 题图)8.(2025·包头)如图,在矩形 ABCD 中,对角线 AC 与 BD 相交于点 O,过点 A 作AE⊥BD,垂足为点 E,若∠EAC=2∠CAD,则∠BAE=__22.5__度.9.(2025·南京)如图,菱形 ABCD 的面积为 120 cm2,正方形 AECF 的面积为 50 cm2,则菱形的边长为___13___cm .,第 9 题图) ,第 10 题图)10.(2025·钦州)如图,在正方形 ABCD 中,E 是 AB 上一点,BE=2,AE=3BE,P 是 AC上一动点,则 PB+PE 的最小值是___10___.三、解答题11.(2025·钦州)如图,在正方形 ABCD 中,E,F 分别是 AB,BC 上的点,且 AE=BF.求证:CE=DF.证明:在正方形 ABCD 中,AB=BC=CD,∠B=∠BCD=90°, AE=BF,∴AB-AE=BC-BF,即 BE=CF,在△BCE 和△CDF 中,∴△BCE≌△CDF(SAS),∴CE=DF12. (2025·云南)如图,菱形 ABCD 的对角线 AC 与 BD 交于点 O,∠ABC∶∠BAD=1∶2,BE∥AC,CE∥BD.(1)求 tan∠DBC 的值;(2)求证:四边形 OBEC 是矩形.解:(1) 四...