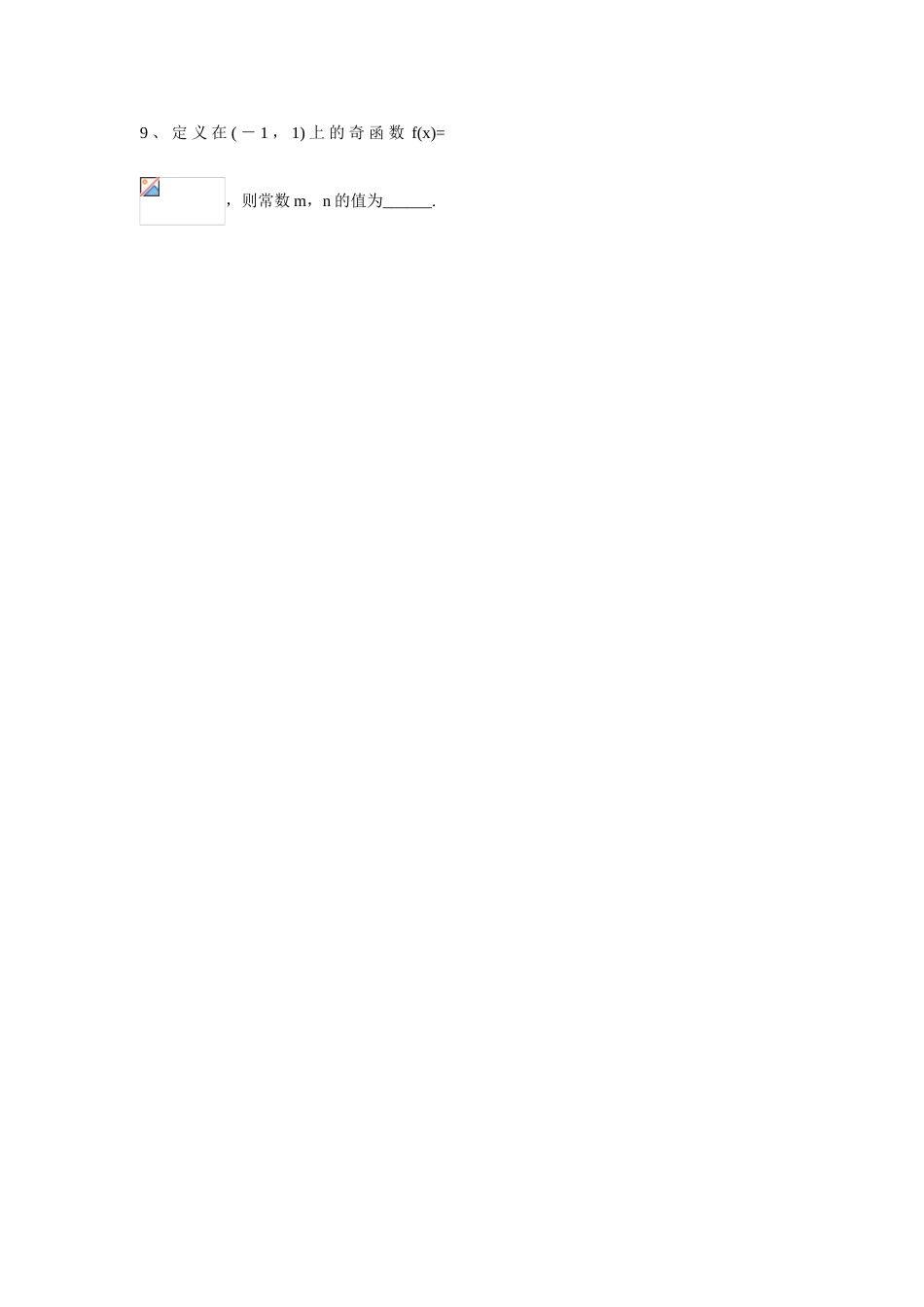
第 12 课 函数的单调性和奇偶性分层训练:1、二次函数 y=ax2+bx+c 的递增区间为(-∞,2],则二次函数 y=bx2+ax+c 的递减区间为( )A.(-∞,]B.[,+∞]C.[2,+∞]D.(-∞,2]2 、 设 f(x) 是 ( - ∞ , +∞) 上 的 奇 函 数 ,f(x+2)= -f(x),当 0≤x≤1 时,f(x)=x,则f(7.5)=( )A.0.5B. -0.5C.1.5D. -1.53、函数 f(x)=(x-1)· ( )A.是奇函数B.是偶函数C.既是奇函数又是偶函数D. 既不是奇函数又不是偶函数4、下列结论正确的是( )A.偶函数的图象一定与 y 轴相交B.奇函数 y=f(x)在 x=0 处有定义,则 f(0)=0C.定义域为 R 的增函数一定是奇函数D.图象过原点的单调函数,一定是奇函数5、设偶函数 y=f(x)(x∈R)在 x<0 时是增函数,若 x1<0,x2>0 且|x1|<|x2|,则下列结论中正确的是( )A.f(-x1)f(-x2)C.f(-x1)=f(-x2)D.以上结论都不对6、若 f(x)满足 f(-x)= -f(x),且在(-∞,0)内是增函数,又 f(-2)=0,则 xf(x)<0 的解集是( )A.(-2,0)∪(0,2)B.(-∞,-2)∪(0,2)C. (-∞,-2) ∪(2,+∞)D.(-2,0) ∪(2,+∞)7、函数 y=(2k+1)x+b 在(-∞,+∞)上是减函数,则 k 的取值范围是_______________.8、函数 y=-在(0,+∞)上是减函数,则y=-2x2+ax 在(0,+∞)上的单调性为_______________.9 、 定 义 在 ( - 1 , 1) 上 的 奇 函 数 f(x)=,则常数 m,n 的值为______.