机械设计课后习题第5章参考答案

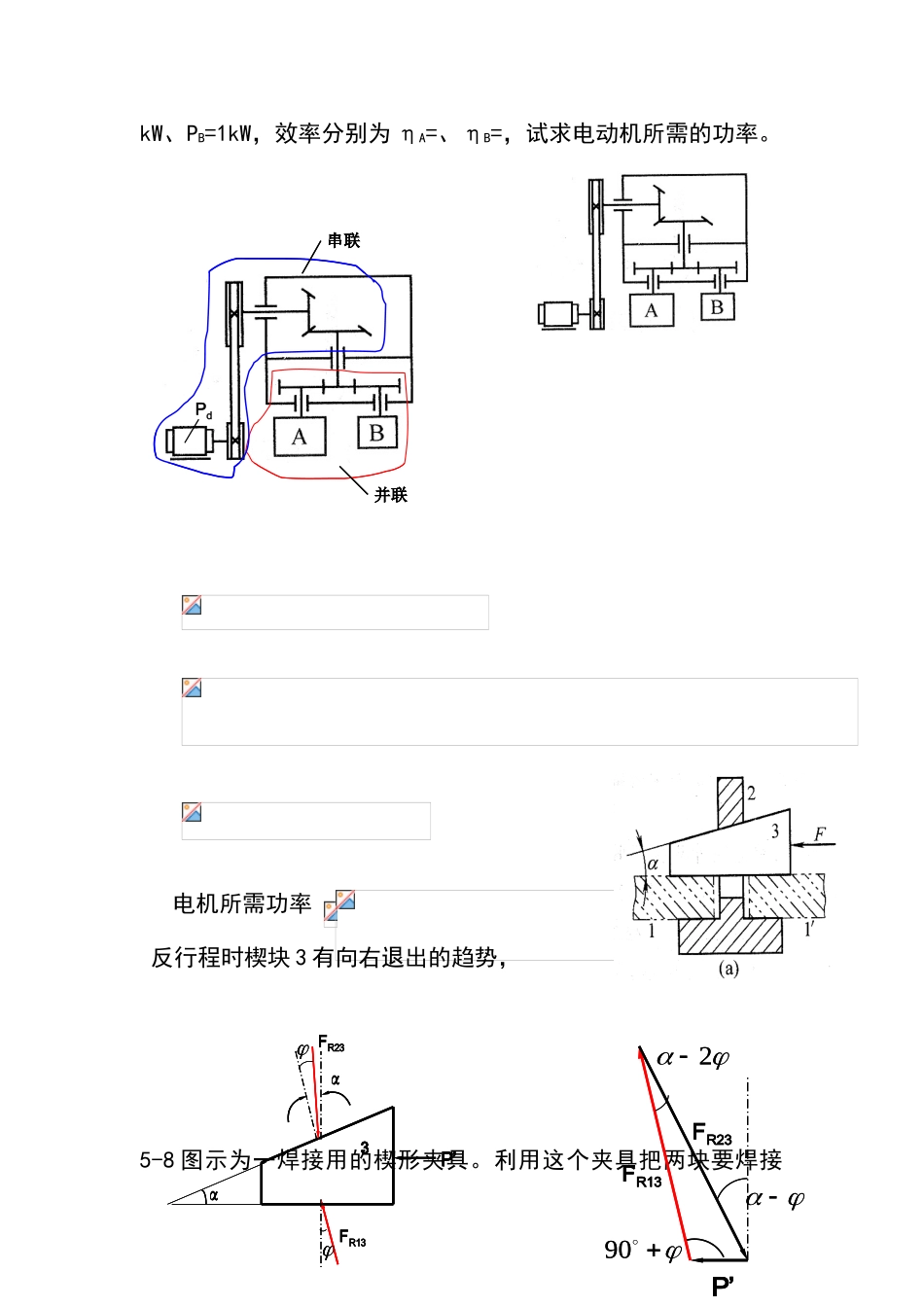
第 5 章 习题解答参考5-6 图示为一带式运输机, 由电动机 1 经平带传动及一个两级齿轮减速器带动运输带 8。设已知运输带 8 所需的曳引力F=5500 N，运送速度 v= m/s。平带传动(包括轴承)的效率η1=，每对齿轮(包括其轴承)的效率 η2=，运输带 8 的机械效率η3=(包括其支承和联轴器)。试求该系统的总效率 η 及电动机所需的功率。解：图示为一串联的传动系统其总效率为：η=η1.η22.η3=ⅹⅹ=电机所需功率：Pd=Fv/η=5500×=8029（W）=（kW）5-7 如图所示，电动机通过 v 带传动及圆锥、圆柱齿轮传动带动工作机 A 及 B。设每对齿轮的效率 η1=(包括轴承的效率在内)，带 传 动 的 效 率 η3= ， 工 作 机 A 、 B 的 功 率 分 别 为 PA=5 解：此传动系统为混联。kW、PB=1kW，效率分别为 ηA=、ηB=，试求电动机所需的功率。电机所需功率 5-8 图示为一焊接用的楔形夹具。利用这个夹具把两块要焊接并联Pd串联并联Pd串联反行程时楔块 3 有向右退出的趋势，P’α3αFR13FR23P’α3αP’α3αFR13FR23P’FR13FR2390 2P’FR13FR2390 2的工件 1 及 1’预先夹妥，以便焊接。图中 2 为夹具体，3 为楔块。试确定其自锁条件(即当夹紧后，楔块 3 不会自动松脱出来的条件)。取楔块 3 为脱离体，根据楔块 3 的平衡条件，作矢量三角形由图分析可知，在反行程 FR23是驱动力，由正弦定理可得, 则于是此机构反行程的效率为令 , 可得自锁条件为 解法二：根据反行程支持力小于或等于零的条件来确定根据楔块 3 的力多边形，由正弦定理可得解法一：根据反行程时 η’≤0的条件确定P’α3αFR13FR23P’α3αP’α3αFR13FR23若楔块不自动松脱，则应使 ，即得自锁条件为解法三：根据移动副的自锁条件确定。由于在反行程 FR23是驱动力，故只要 FR23作用在摩擦角 φ 内，楔块 3 即发生自锁。即 因此可得自锁条件为解法四：根据驱动力的有效分力始终小于阻力的有效分力确定 由于在反行程 FR23是驱动力，FR13是阻力由正弦定理 即 自锁条件为 即 可得自锁条件为 P’α3αFR13FR23P’α3αP’α3αFR13FR23P’FR13FR2390 2P’FR13FR2390 2