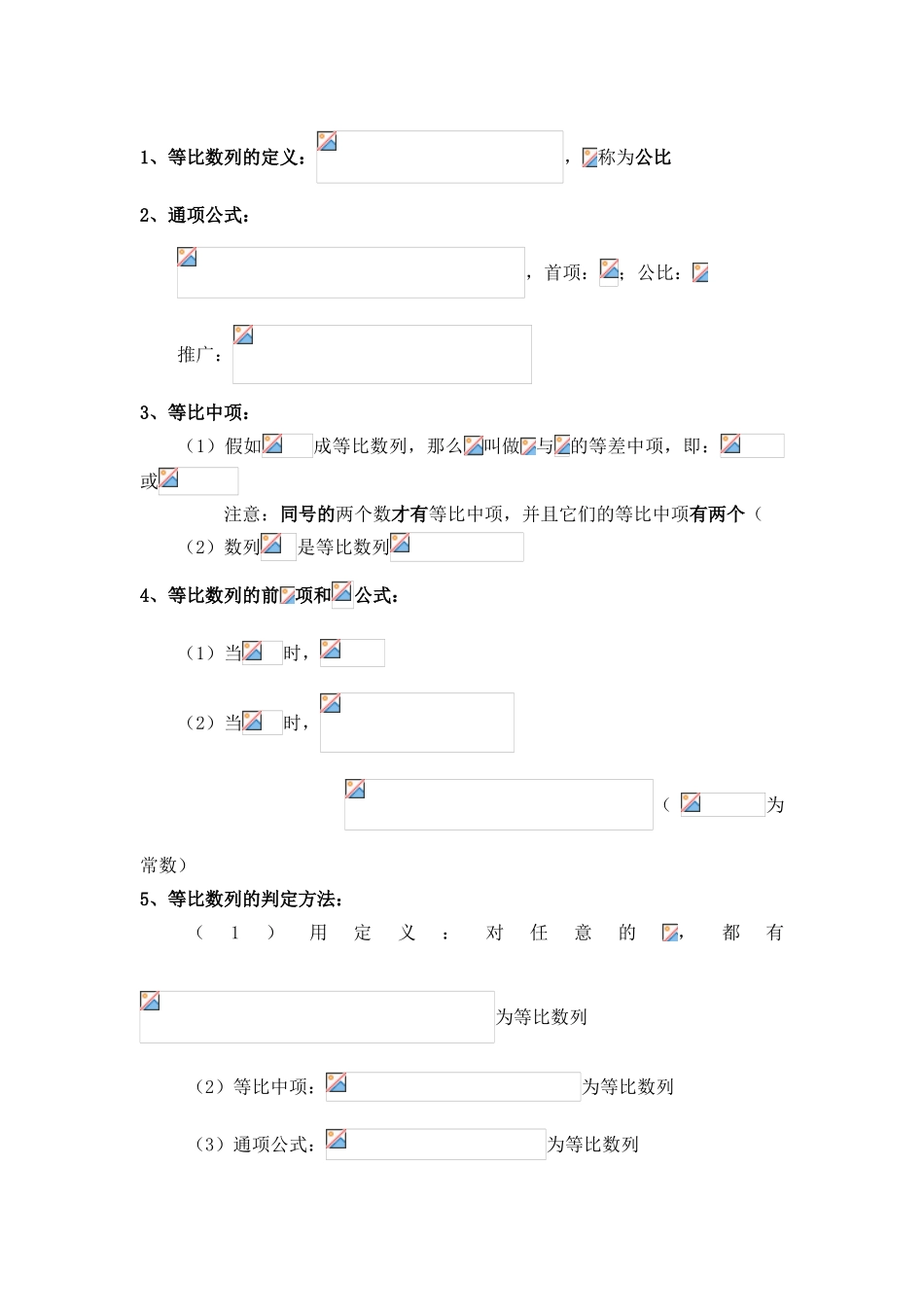
1、等比数列的定义:,称为公比2、通项公式:,首项:;公比:推广:3、等比中项:(1)假如成等比数列,那么叫做与的等差中项,即:或注意:同号的两个数才有等比中项,并且它们的等比中项有两个((2)数列是等比数列4、等比数列的前项和公式:(1)当时,(2)当时,(为常数)5、等比数列的判定方法:(1)用定义:对任意的,都有为等比数列(2)等比中项:为等比数列(3)通项公式:为等比数列6、等比数列的证明方法:依据定义:若或为等比数列7、等比数列的性质:(2)对任何,在等比数列中,有。(3)若,则。特别的,当时,得 注:(4)数列,为等比数列,则数列,,,,(为非零常数)均为等比数列。(5)数列为等比数列,每隔项取出一项仍为等比数列(6)假如是各项均为正数的等比数列,则数列是等差数列(7)若为等比数列,则数列,,,成等比数列( 8 ) 若为 等 比 数 列 , 则 数 列,,成等比数列(9)①当时, ② 当时,③ 当时,该数列为常数列(此时数列也为等差数列);④ 当时,该数列为摆动数列.(10)在等比数列中,当项数为时,二 例题解析【例 1】 已知 Sn 是数列{an}的前 n 项和,Sn=pn(p∈R,n∈N*),那么数列{an}.( )A.是等比数列 B.当 p≠0 时是等比数列B.C.当 p≠0,p≠1 时是等比数列 D.不是等比数列【例2】已知等比数列 1,x1,x2,…,x2n,2,求 x1·x2·x3·…·x2n.式;(2)已知 a3·a4·a5=8,求 a2a3a4a5a6 的值.【例 4】 求数列的通项公式:(1){an}中,a1=2,an+1=3an+2(2){an}中,a1=2,a2=5,且 an+2-3an+1+2an=0三、 考点分析考点一:等比数列定义的应用1、数列满足,,则_________.2、在数列中,若,,则该数列的通项______________.考点二:等比中项的应用1、已知等差数列的公差为,若,,成等比数列,则( )A . B . C . D.2、若、、 成等比数列,则函数的图象与轴交点的个数为( )A.B. C.D.不确定3、已知数列为等比数列,,,求的通项公式.考点三:等比数列及其前 n 项和的基本运算1、若公比为的等比数列的首项为,末项为,则这个数列的项数是( )A. B. C. D.2、已知等比数列中,,,则该数列的通项_________________.3、若为等比数列,且,则公比________.4、设,,,成等比数列,其公比为,则的值为( )A.B. C. D.5 、 等 比 数 列 {an} 中 , 公 比 q=且 a2+a4+…+a100=30 ,...