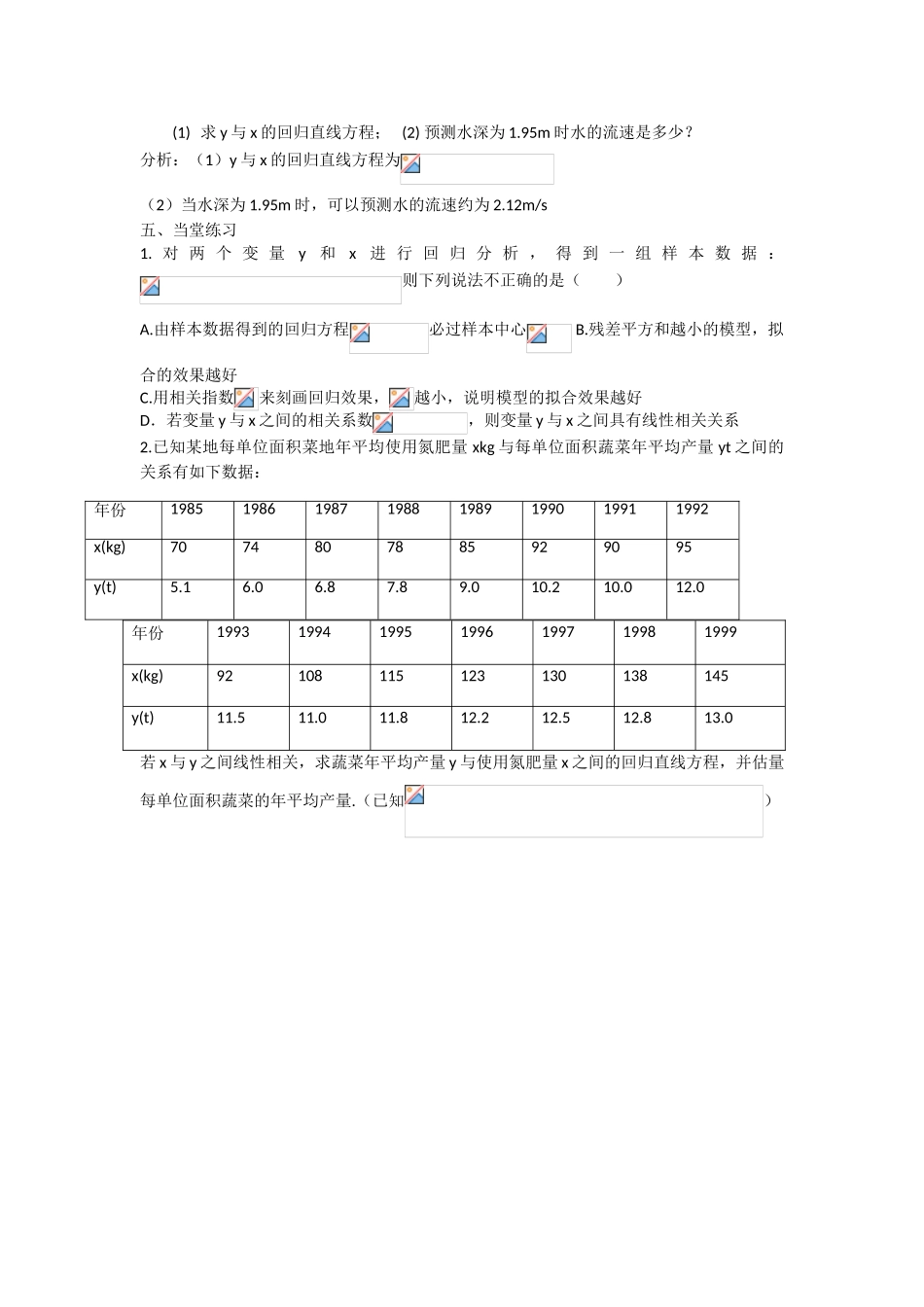
3.1.1 回归分析的基本思想及其初步应用课前预习学案一、预习目标通过截距与斜率分别是使取最小值时,求的值。二、预习内容:1.对于一组具有线性相关关系的数据其回归直线方程的截距和斜率的最小二乘法估量公式:= ,= 2.= , = 3.样本点的中心 三、提出问题如何使 值最小,通过观察分析式子进行试探推到课内探究学案一、学习目标1.了解回归分析的基本思想和方法 , 培育学生观察分析计算的能力二、学习重难点学习重点:回归方程,学习难点:、公式的推到三、学习过程1.使值最小时,值的推到2.结论 3.中和的含义是什么4. 一定通过回归方程吗?四、典型例题例 1.讨论某灌溉倒水的流速 y 与水深 x 之间的关系,测得一组数据如下:水深 x(m)1.401.501.601.701.801.902.002.10流速 y(m/s)1.701.791.881.952.032.102.162.21(1) 求 y 与 x 的回归直线方程; (2) 预测水深为 1.95m 时水的流速是多少?分析:(1)y 与 x 的回归直线方程为(2)当水深为 1.95m 时,可以预测水的流速约为 2.12m/s五、当堂练习1. 对 两 个 变 量y和x进 行 回 归 分 析 , 得 到 一 组 样 本 数 据 :则下列说法不正确的是( )A.由样本数据得到的回归方程必过样本中心 B.残差平方和越小的模型,拟合的效果越好C.用相关指数来刻画回归效果,越小,说明模型的拟合效果越好D.若变量 y 与 x 之间的相关系数,则变量 y 与 x 之间具有线性相关关系2.已知某地每单位面积菜地年平均使用氮肥量 xkg 与每单位面积蔬菜年平均产量 yt 之间的关系有如下数据:年份1993199419951996199719981999x(kg)92108115123130138145y(t)11.511.011.812.212.512.813.0若 x 与 y 之间线性相关,求蔬菜年平均产量 y 与使用氮肥量 x 之间的回归直线方程,并估量每单位面积蔬菜的年平均产量.(已知) 年份19851986198719881989199019911992x(kg)7074807885929095y(t)5.16.06.87.89.010.210.012.0 课后练习与提高1、 下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量 x(吨)与相应的生产能耗 y(吨标准煤)的几组对比数据:x3456y2.5344.5(1) 请画出上表数据的散点图;(2) 请根据上表提供的数据,用最小二乘法求出 y 关于 x 的线性回归方程;(3) 已知该厂技改前 100 吨甲产品的生产能耗为 90 吨标准煤,试根据(2)求出的线性回归方程,预测生产 100 吨甲产品的生产能耗比技改前降低多少吨标准煤?(参考数值:)解:(1)由题设所给数据,可得散点图如下图 O 1 2 3 4 5 6 x( 产量:吨 )y( 能耗 : 吨标准煤 ) 4.5 4 3 2.5