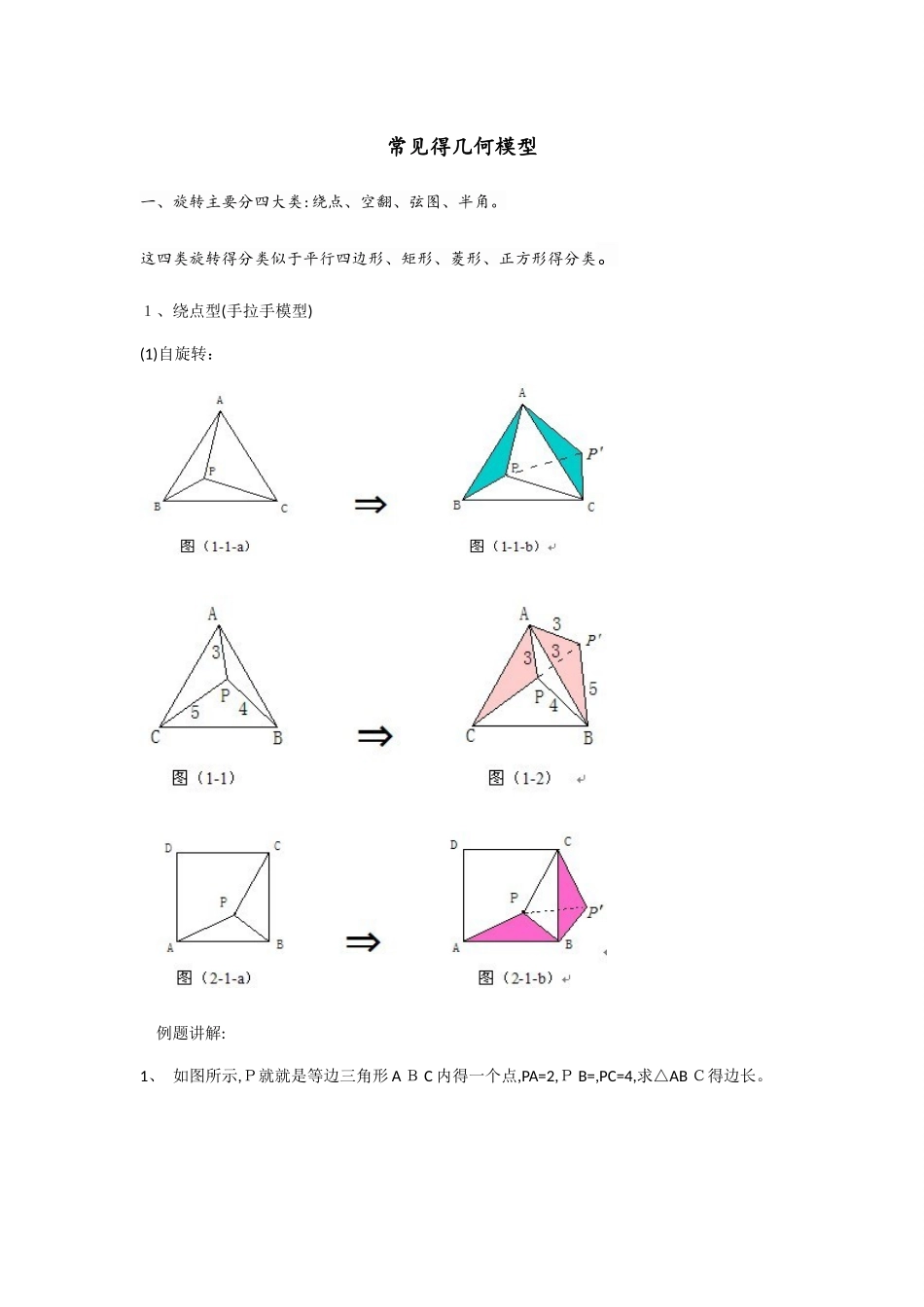
常见得几何模型一、旋转主要分四大类:绕点、空翻、弦图、半角。这四类旋转得分类似于平行四边形、矩形、菱形、正方形得分类。1、绕点型(手拉手模型)(1)自旋转:例题讲解:1、 如图所示,P就就是等边三角形 A B C 内得一个点,PA=2,P B=,PC=4,求△AB C得边长。 2、 如图,O 就就是等边三角形 A B C 内一点,已知:AOB=115°∠,∠BOC=12 5°,则以线段OA、O B、O C 为边构成三角形得各角度数就就是多少?3、如图,P 就就是正方形 ABCD 内一点,且满足 PA:PD:PC=1:2:3,则∠A P D= 、 4、如图(2-1):P 就就是正方形A BCD 内一点,点 P 到正方形得三个顶点 A、B、C得距离分别为P A=1,PB=2,PC=3。求此正方形AB C D面积。(2)共旋转(典型得手拉手模型)模型变形:ABCOCABP例题讲解: 1、 已知△A B C 为等边三角形,点 D 为直线 BC 上得一动点(点 D 不与 B,C 重合),以 AD为边作菱形ADE F(按 A,D,E,F 逆时针排列),使∠DAF=6 0°,连接C F、(1) 如图 1,当点D在边B C 上时,求证:① BD=CF ‚ ②AC=CF+C D、(2)如图 2,当点D在边 BC 得延长线上且其她条件不变时,结论A C=CF+CD 就就是否成立?若不成立,请写出 AC、CF、C D之间存在得数量关系,并说明理由; (3)如图 3,当点D在边 BC 得延长线上且其她条件不变时,补全图形,并直接写出AC、CF、C D之间存在得数量关系。等边三角形共顶点共顶点等腰直角三角形共顶点等腰三角形共顶点等腰三角形2、(13 北京中考)在△AB C 中,AB=A C,∠B A C=(),将线段 BC 绕点 B 逆时针旋转 6 0°得到线段B D。(1)如图 1,直接写出∠ABD 得大小(用含得式子表示);(2)如图2,∠BCE=1 5 0°,∠AB E=60°,推断△A B E 得形状并加以证明;(3)在(2)得条件下,连结 DE,若∠DEC=4 5°,求得值。2、半角模型说明:旋转半角得特征就就是相邻等线段所成角含一个二分之一角,通过旋转将另外两个与为二分之一得角拼接在一起,成对称全等。例题:1、在等腰直角△ABCD 得斜边上取两点M,N,使得,记A M=m,MN=x,BN=n,求证以 m,x,n 为边长得三角形为直角三角形。2、如图,正方形 ABCD 得边长为 1,A B,A D 上各存在一点 P、Q,若△A PQ 得周长为 2,求得度数。3、、分别就就是正方形得边、上得点,且,,为垂足,求证:、4、 已知,正方形 AB C D 中,∠M A N=45°,∠M A N绕点...