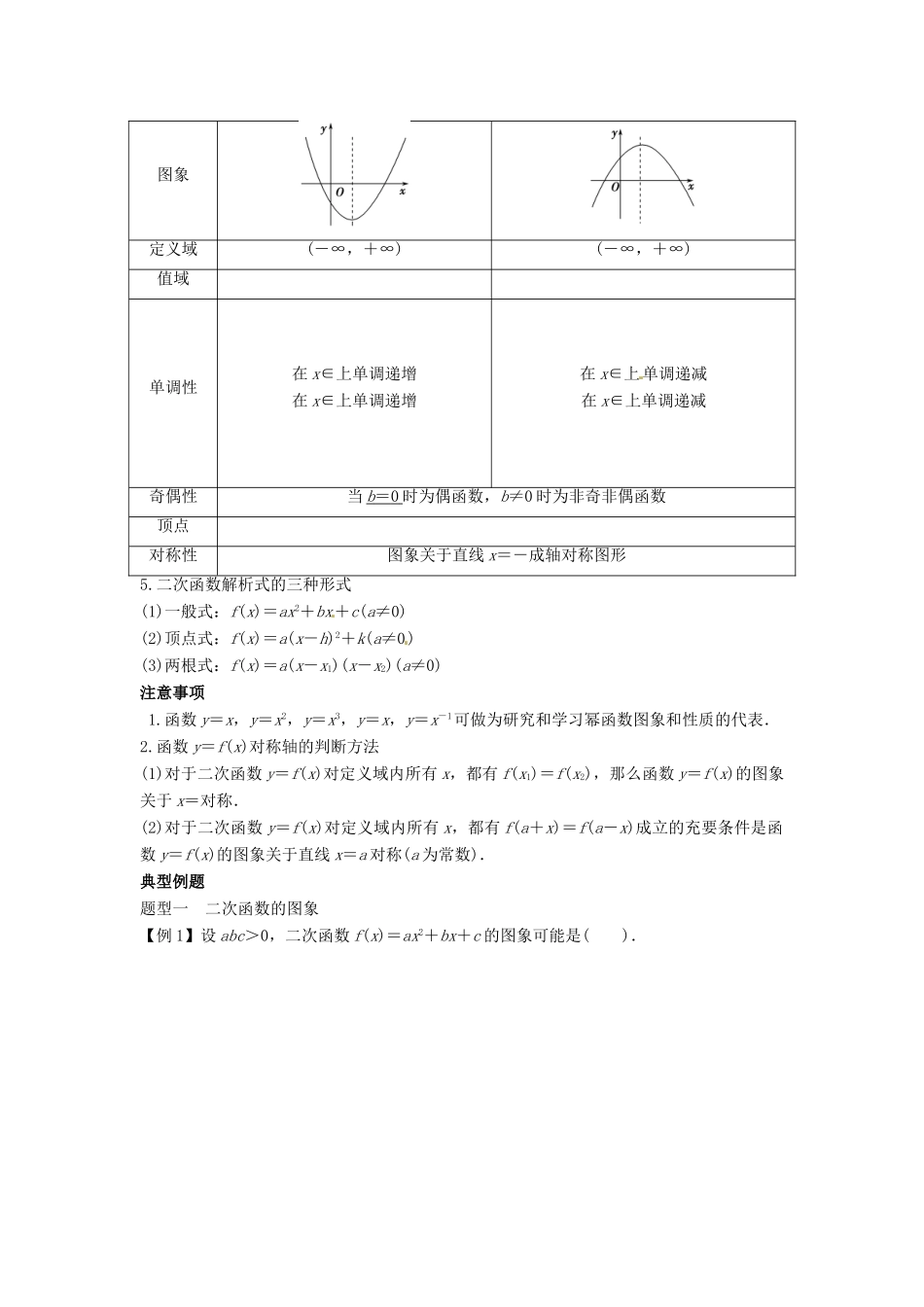
2.6 幂函数与二次函数考情分析1.求二次函数的解析式.2.求二次函数的值域与最值.3.利用幂函数的图象和性质分析解决有关问题.基础知识1.幂函数的定义一般地,形如 y = x α (α∈R)的函数称为幂函数,其中底数 x 是自变量,α 为常数.2.幂函数的图象在同一平面直角坐标系下,幂函数 y=x,y=x2,y=x3,y=x,y=x-1的图象分别如右图.3.幂函数的性质y=xy=x2y=x3y=xy=x-1定义域RRR[0 ,+∞ ) {x|x∈R 且 x≠0}值 域R[0,+∞)R[0,+∞){y|y∈R 且 y≠0}奇偶性奇偶奇非奇非偶奇单调性增x∈[0,+∞)时,增x∈(-∞,0]时,减增增x∈(0,+∞)时,减x∈(-∞,0)时,减定点(0,0) , (1,1) (1,1)4.二次函数的图象和性质解析式f(x)=ax2+bx+c(a>0)f(x)=ax2+bx+c(a<0)图象定义域(-∞,+∞)(-∞,+∞)值域单调性在 x∈上单调递增在 x∈上单调递增在 x∈上单调递减在 x∈上单调递减奇偶性当 b = 0 时为偶函数,b≠0 时为非奇非偶函数顶点对称性图象关于直线 x=-成轴对称图形5.二次函数解析式的三种形式(1)一般式:f(x)=ax2+bx+c(a≠0)(2)顶点式:f(x)=a(x-h)2+k(a≠0)(3)两根式:f(x)=a(x-x1)(x-x2)(a≠0)注意事项 1.函数 y=x,y=x2,y=x3,y=x,y=x-1可做为研究和学习幂函数图象和性质的代表.2.函数 y=f(x)对称轴的判断方法(1)对于二次函数 y=f(x)对定义域内所有 x,都有 f(x1)=f(x2),那么函数 y=f(x)的图象关于 x=对称.(2)对于二次函数 y=f(x)对定义域内所有 x,都有 f(a+x)=f(a-x)成立的充要条件是函数 y=f(x)的图象关于直线 x=a 对称(a 为常数).典型例题题型一 二次函数的图象【例 1】设 abc>0,二次函数 f(x)=ax2+bx+c 的图象可能是( ).解析 若 a>0,则 bc>0,根据选项 C、D,c<0,此时只有 b<0,二次函数的对称轴方程x=->0,选项 D 有可能;若 a<0,根据选项 A,c<0,此时只能 b>0,二次函数的对称轴方程 x=->0,与选项 A 不符合;根据选项 B,c>0,此时只能 b<0,此时二次函数的对称轴方程 x=-<0,与选项 B 不符合.综合知只能是选项 D.答案 D【变式 1】 已知二次函数 f(x)的图象如图所示,则其导函数 f′(x)的图象的大致形状是( ).解析 由函数 f(x)的图象知:当 x∈(-∞,1]时,f(x)为减函数,∴f′(x)≤0;当x∈[1,+∞)时,f(x)为增函数,∴f′(x)≥0.结合选项知选...