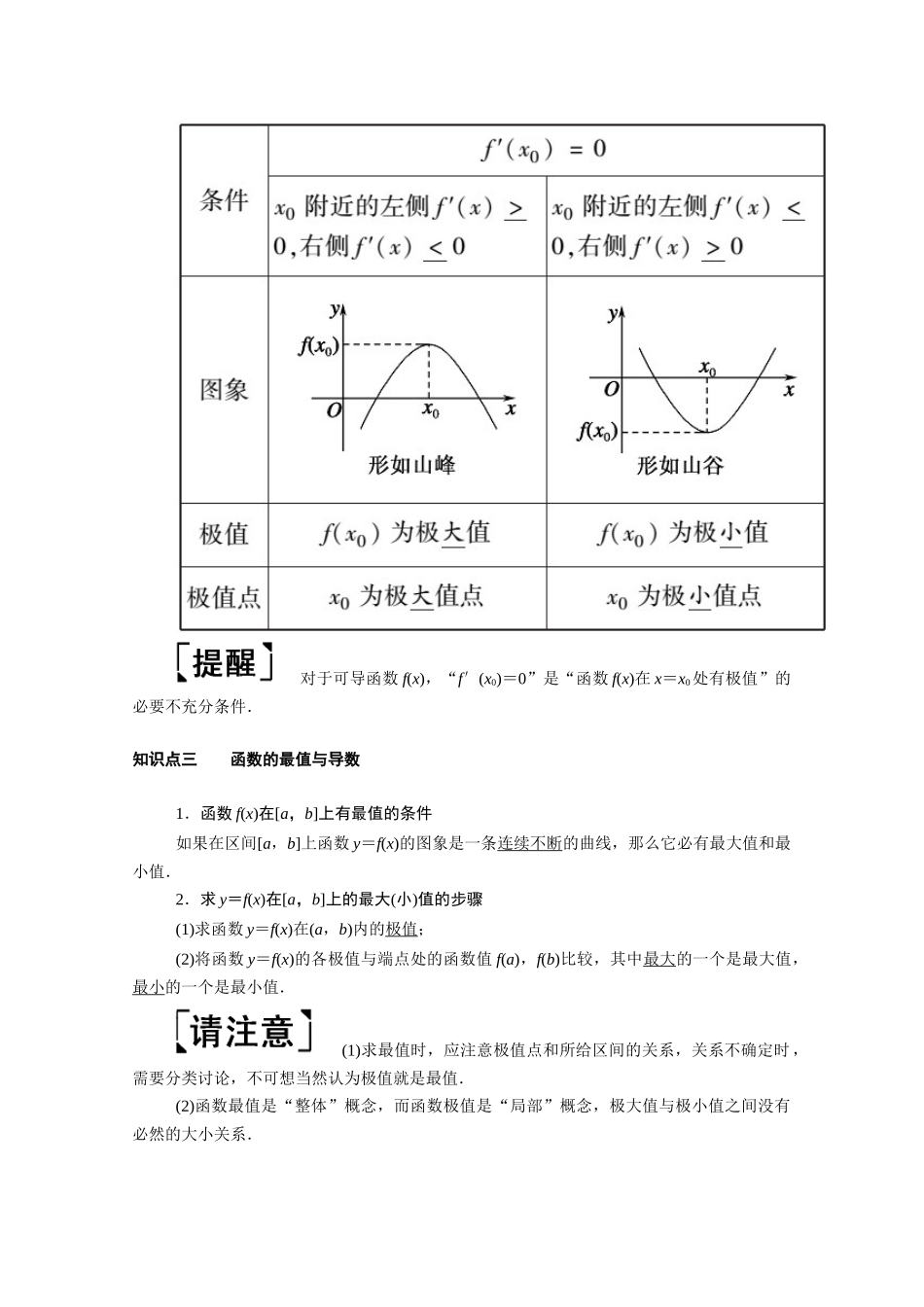
第十一节 导数的简单应用课标要求考情分析1.了解函数的单调性与导数的关系;能利用导数研究函数的单调性,会求函数的单调区间(其中多项式函数不超过三次).2.了解函数在某点取得极值的必要条件和充分条件;会用导数求函数的极大值、极小值(其中多项式函数不超过三次);会求闭区间上函数的最大值、最小值(其中多项式函数不超过三次).1.利用导数求函数的单调区间及极值(最值)、结合单调性与不等式的成立情况求参数范围是高考命题的热点.2.常与基本初等函数的图象与性质、解析几何、不等式、方程等交汇命题,主要考查转化与化归思想、分类讨论思想的应用.3.题型主要以解答题为主,属中高档题. 知识点一 函数的单调性与导数的关系函数 y=f(x)在某个区间内可导,则:(1)若 f′(x)>0,则 f(x)在这个区间内单调递增;(2)若 f′(x)<0,则 f(x)在这个区间内单调递减;(3)若 f′(x)=0,则 f(x)在这个区间内是常数函数.函数 f(x)在区间(a,b)上递增,则 f′(x)≥0,“f′(x)>0 在(a,b)上成立”是“f(x)在(a,b)上单调递增”的充分不必要条件.知识点二 函数的极值与导数对于可导函数 f(x),“f′(x0)=0”是“函数 f(x)在 x=x0处有极值”的必要不充分条件.知识点三 函数的最值与导数1.函数 f(x)在[a,b]上有最值的条件如果在区间[a,b]上函数 y=f(x)的图象是一条连续不断的曲线,那么它必有最大值和最小值.2.求 y=f(x)在[a,b]上的最大(小)值的步骤(1)求函数 y=f(x)在(a,b)内的极值;(2)将函数 y=f(x)的各极值与端点处的函数值 f(a),f(b)比较,其中最大的一个是最大值,最小的一个是最小值.(1)求最值时,应注意极值点和所给区间的关系,关系不确定时,需要分类讨论,不可想当然认为极值就是最值.(2)函数最值是“整体”概念,而函数极值是“局部”概念,极大值与极小值之间没有必然的大小关系.1.思考辨析判断下列结论正误(在括号内打“√”或“×”)(1)若函数 f(x)在(a,b)内单调递增,那么一定有 f′(x)>0.( × )(2)如果函数 f(x)在某个区间内恒有 f′(x)=0,则 f(x)在此区间内没有单调性.( √ )(3)函数的极大值一定大于其极小值.( × )(4)对可导函数 f(x),f′(x0)=0 是 x0为极值点的充要条件.( × )(5)函数的最大值不一定是极大值,函数的最小值也不一定是极小值.( √ )解析:(1)f(x)在(a,b)内单调递增,则有 f′(x)≥0.(3)函数的极大值也可能小于极小值.(4)x0为 f(x)的极值点...