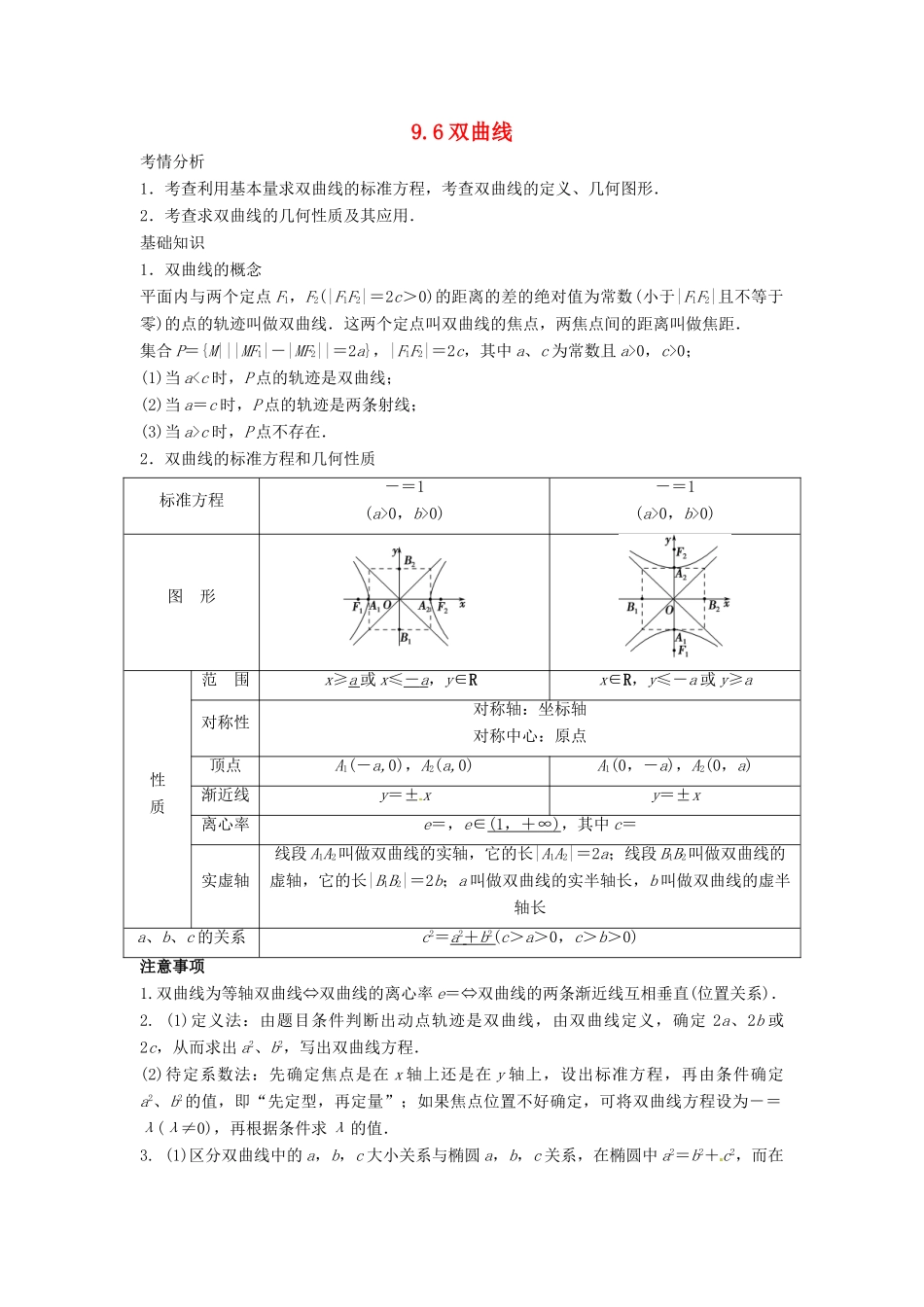
9.6 双曲线考情分析1.考查利用基本量求双曲线的标准方程,考查双曲线的定义、几何图形.2.考查求双曲线的几何性质及其应用.基础知识1.双曲线的概念平面内与两个定点 F1,F2(|F1F2|=2c>0)的距离的差的绝对值为常数(小于|F1F2|且不等于零)的点的轨迹叫做双曲线.这两个定点叫双曲线的焦点,两焦点间的距离叫做焦距.集合 P={M|||MF1|-|MF2||=2a},|F1F2|=2c,其中 a、c 为常数且 a>0,c>0;(1)当 ac 时,P 点不存在.2.双曲线的标准方程和几何性质标准方程-=1(a>0,b>0)-=1(a>0,b>0)图 形性 质范 围x≥a 或 x≤- a ,y∈R[x∈R,y≤-a 或 y≥a对称性对称轴:坐标轴对称中心:原点顶点A1(-a,0),A2(a,0)A1(0,-a),A2(0,a)渐近线y=±xy=±x离心率e=,e∈(1 ,+∞ ) ,其中 c=实虚轴线段 A1A2叫做双曲线的实轴,它的长|A1A2|=2a;线段 B1B2叫做双曲线的虚轴,它的长|B1B2|=2b;a 叫做双曲线的实半轴长,b 叫做双曲线的虚半轴长a、b、c 的关系c2=a 2 + b 2 (c>a>0,c>b>0)注意事项1.双曲线为等轴双曲线⇔双曲线的离心率 e=⇔双曲线的两条渐近线互相垂直(位置关系).2. (1)定义法:由题目条件判断出动点轨迹是双曲线,由双曲线定义,确定 2a、2b 或2c,从而求出 a2、b2,写出双曲线方程.(2)待定系数法:先确定焦点是在 x 轴上还是在 y 轴上,设出标准方程,再由条件确定a2、b2的值,即“先定型,再定量”;如果焦点位置不好确定,可将双曲线方程设为-=λ(λ≠0),再根据条件求 λ 的值.3. (1)区分双曲线中的 a,b,c 大小关系与椭圆 a,b,c 关系,在椭圆中 a2=b2+c2,而在双曲线中 c2=a2+b2.(2)双曲线的离心率大于 1,而椭圆的离心率 e∈(0,1).(3)双曲线-=1(a>0,b>0)的渐近线方程是 y=±x,-=1(a>0,b>0)的渐近线方程是 y=±x.题型一 双曲线定义的应用【例 1】设 F1、F2分别是双曲线 x2-=1 的左、右焦点.若点 P 在双曲线上,且|PF1|=5,则|PF2|=( )A. 5 B. 3C. 7 D. 3 或 7答案:D解析: ||PF1|-|PF2||=2,∴|PF2|=7 或 3.【变式 1】在平 面直角坐标系 xOy 中,已知双曲线-=1 上一点 M 的横坐标为 3,则点 M 到此双曲线的右焦点的距离为________.解析 由题易知,双曲线的右焦点为(4,0),点 M 的坐标为(3,)...