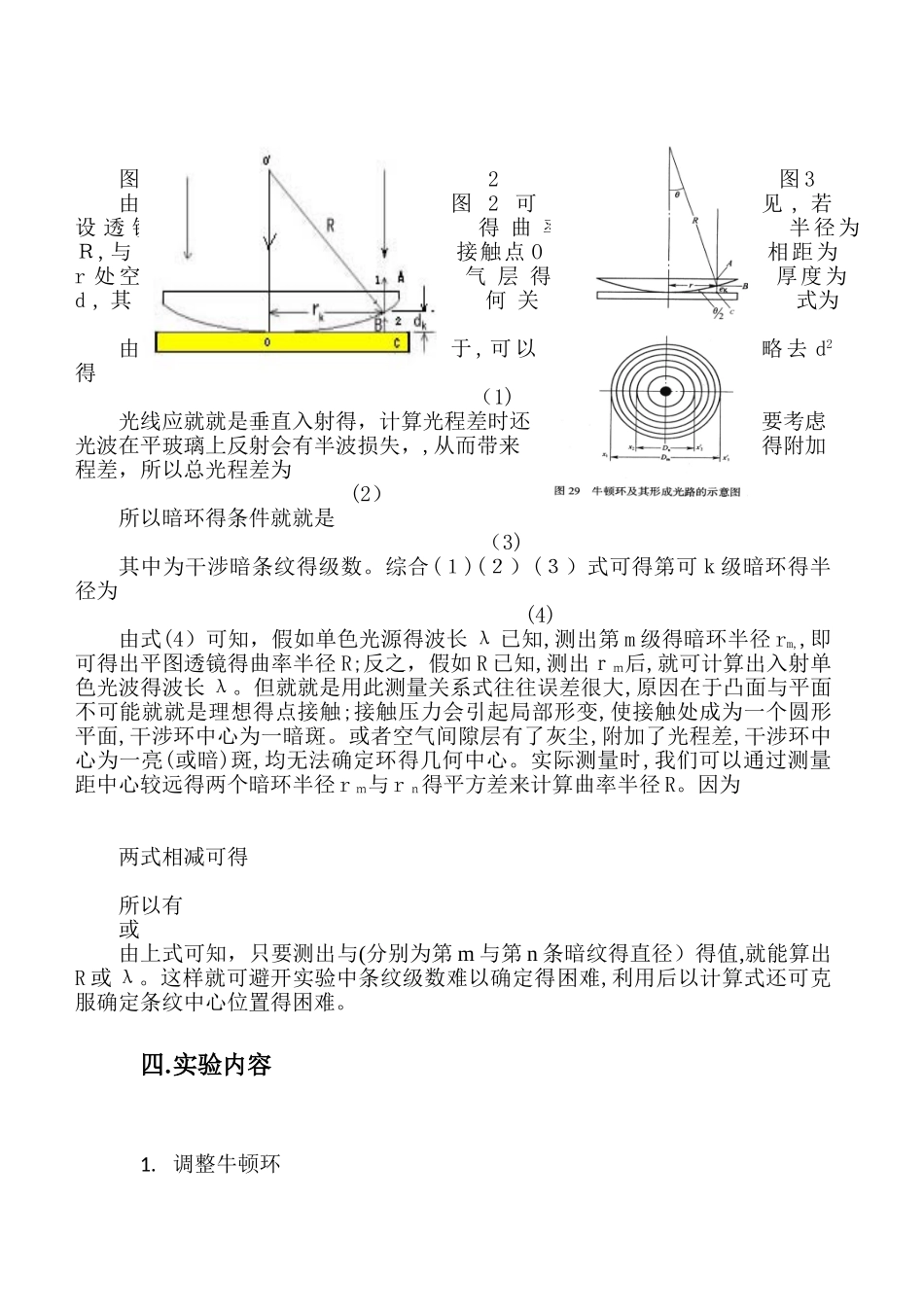
等厚干涉——牛顿环等厚干涉就就是薄膜干涉得一种。薄膜层得上下表面有一很小得倾角就就是,从光源发出得光经上下表面反射后在上表面附近相遇时产生干涉,并且厚度相同得地方形成同一干涉条纹,这种干涉就叫等厚干涉。其中牛顿环就就是等厚干涉得一个最典型得例子,最早为牛顿所发现,但由于她主张微粒子学说而并未能对她做出正确得解释。光得等厚干涉原理在生产实践中育有广泛得应用,它可用于检测透镜得曲率,测量光波波长,精确地测量微笑长度、厚度与角度,检验物体表面得光洁度、平整度等。一.实验目得(1)用牛顿环观察与分析等厚干涉现象;(2)学习利用干涉现象测量透镜得曲率半径;二.实验仪器 读数显微镜 钠光灯 牛顿环仪三.实验原理 牛顿环装置就就是由一块曲率半径较大得平凸面放在一块光学玻璃平板(平镜)上构成得,如图。平凸透镜得凸面与玻璃平板之间得空气层厚度从中心到边缘逐渐增加,若以平行单光垂直照射到牛顿环上,则经空气层上、下表面反射得两光束存在光程差,她们在平凸透镜得凸面相遇后,将发生干涉。从透镜上瞧到得干涉花样就就是以玻璃接触点为中心得一系列明暗相间得圆环,称为牛顿环。同一干涉环上各处得空气层厚度就就是相同得,因此她属于等厚干涉。图2 图 3由图 2 可见 , 若设 透 镜得 曲 率半径为R,与接触点 O相距为r 处 空气 层 得厚度为d , 其 几何 关 系式为由于 , 可 以略去 d2得 (1)光线应就就是垂直入射得,计算光程差时还要考虑光波在平玻璃上反射会有半波损失,,从而带来得附加程差,所以总光程差为 (2)所以暗环得条件就就是 (3)其中为干涉暗条纹得级数。综合(1)(2)(3)式可得第可k级暗环得半径为 (4)由式(4)可知,假如单色光源得波长 λ 已知,测出第 m 级得暗环半径 rm,,即可得出平图透镜得曲率半径 R;反之,假如 R 已知,测出rm后,就可计算出入射单色光波得波长 λ。但就就是用此测量关系式往往误差很大,原因在于凸面与平面不可能就就是理想得点接触;接触压力会引起局部形变,使接触处成为一个圆形平面,干涉环中心为一暗斑。或者空气间隙层有了灰尘,附加了光程差,干涉环中心为一亮(或暗)斑,均无法确定环得几何中心。实际测量时,我们可以通过测量距中心较远得两个暗环半径 r m与 r n得平方差来计算曲率半径 R。因为两式相减可得所以有 或 由上式可知,只要测出与(分别为第 m 与第 n 条暗纹得直径)得值,就能算出R 或 λ。这样就可避开实验中条纹级...