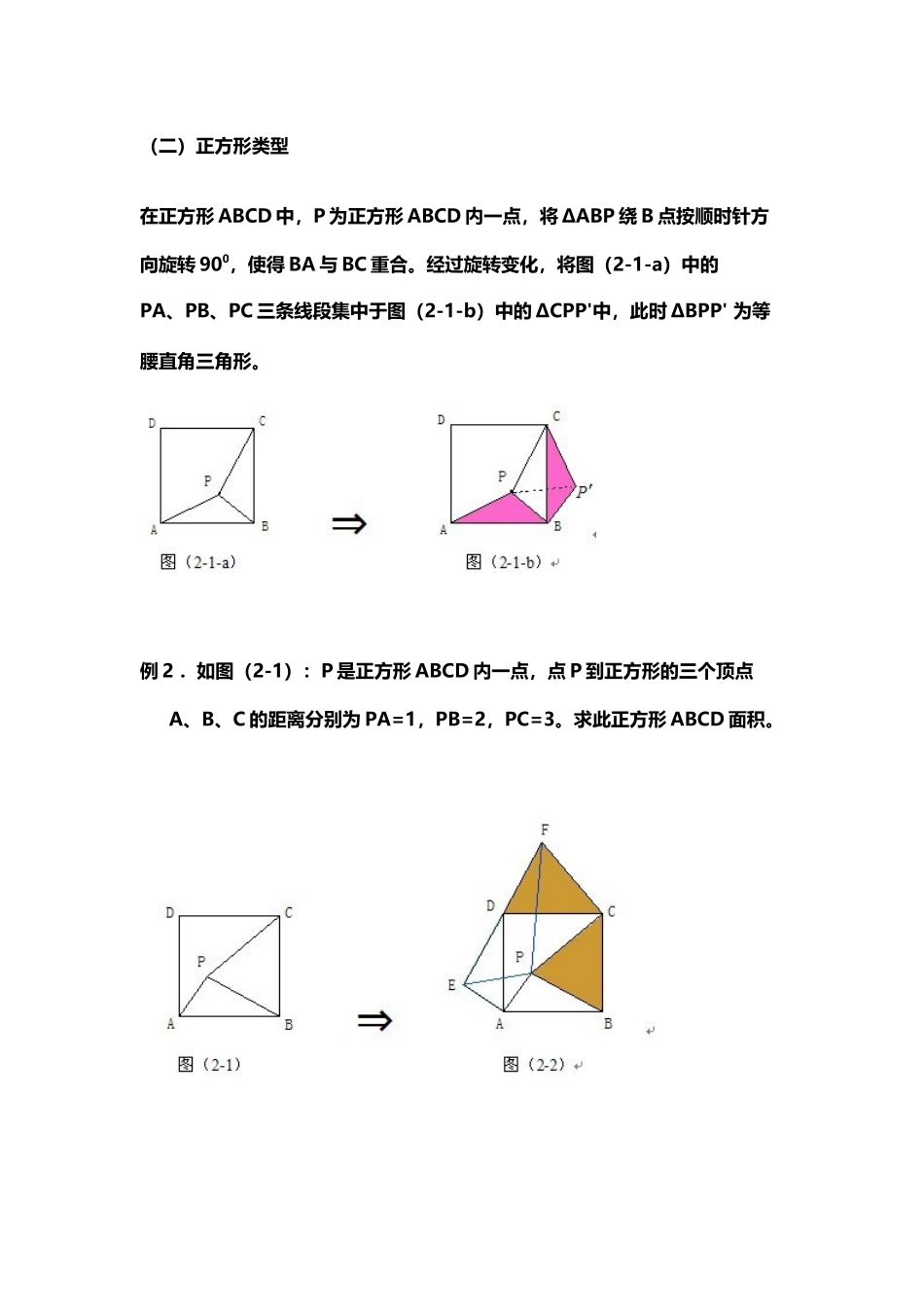
中考常考的旋转、折叠、翻转等几种经典类型(17 页)Good is good, but better carries it.精益求精,善益求善。中考常考题型(一)正三角形类型在正 ΔABC 中,P 为 ΔABC 内一点,将 ΔABP 绕 A 点按逆时针方向旋转 600,使得 AB 与AC 重合。经过这样旋转变化,将图(1-1-a)中的 PA、PB、PC 三条线段集中于图(1-1-b)中的一个 ΔP'CP 中,此时 ΔP'AP 也为正三角形。例 1. 如图:(1-1):设 P 是等边 ΔABC 内的一点,PA=3, PB=4,PC=5,∠APB 的度数是________.(二)正方形类型在正方形 ABCD 中,P 为正方形 ABCD 内一点,将 ΔABP 绕 B 点按顺时针方向旋转 900,使得 BA 与 BC 重合。经过旋转变化,将图(2-1-a)中的PA、PB、PC 三条线段集中于图(2-1-b)中的 ΔCPP'中,此时 ΔBPP' 为等腰直角三角形。例 2 . 如图(2-1):P 是正方形 ABCD 内一点,点 P 到正方形的三个顶点A、B、C 的距离分别为 PA=1,PB=2,PC=3。求此正方形 ABCD 面积。 (三)等腰直角三角形类型 在等腰直角三角形 ΔABC 中, ∠C=Rt∠ , P 为 ΔABC 内一点,将 ΔAPC绕 C 点按逆时针方向旋转 900,使得 AC 与 BC 重合。经过这样旋转变化,在图(3-1-b)中的一个 ΔP' CP 为等腰直角三角形。 例 3.如图,在 ΔABC 中,∠ ACB =900,BC=AC,P 为 ΔABC 内一点,且PA=3,PB=1,PC=2。求∠ BPC 的度数。平移、旋转和翻折是几何变换中的三种基本变换。所谓几何变换就是根据确定的法则,对给定的图形(或其一部分)施行某种位置变化,然后在新的图形中分析有关图形之间的关系.这类实体的特点是:结论开放,注重考查学生的猜想、探究能力;便于与其它知识相联系,解题灵活多变,能够考察学生分析问题和解决问题的能力.在这一理念的引导下,近几年中考加大了这方面的考察力度,特别是 2025 年中考,这一部分的分值比前两年大幅度提高。 为帮助广阔考生把握好平移,旋转和翻折的特征,巧妙利用平移,旋转和翻折的知识来解决相关的问题,下面以近几年中考题为例说明其解法,供大家参考。一.平移、旋转平移:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.“一定的方向”称为平移方向,“一定的距离”称为平移距离。平移特征:图形平移时,图形中的每一点的平移方向都相同,平移距离都相等。旋转:在平面内,将一个图形绕一个定点沿某个方向...