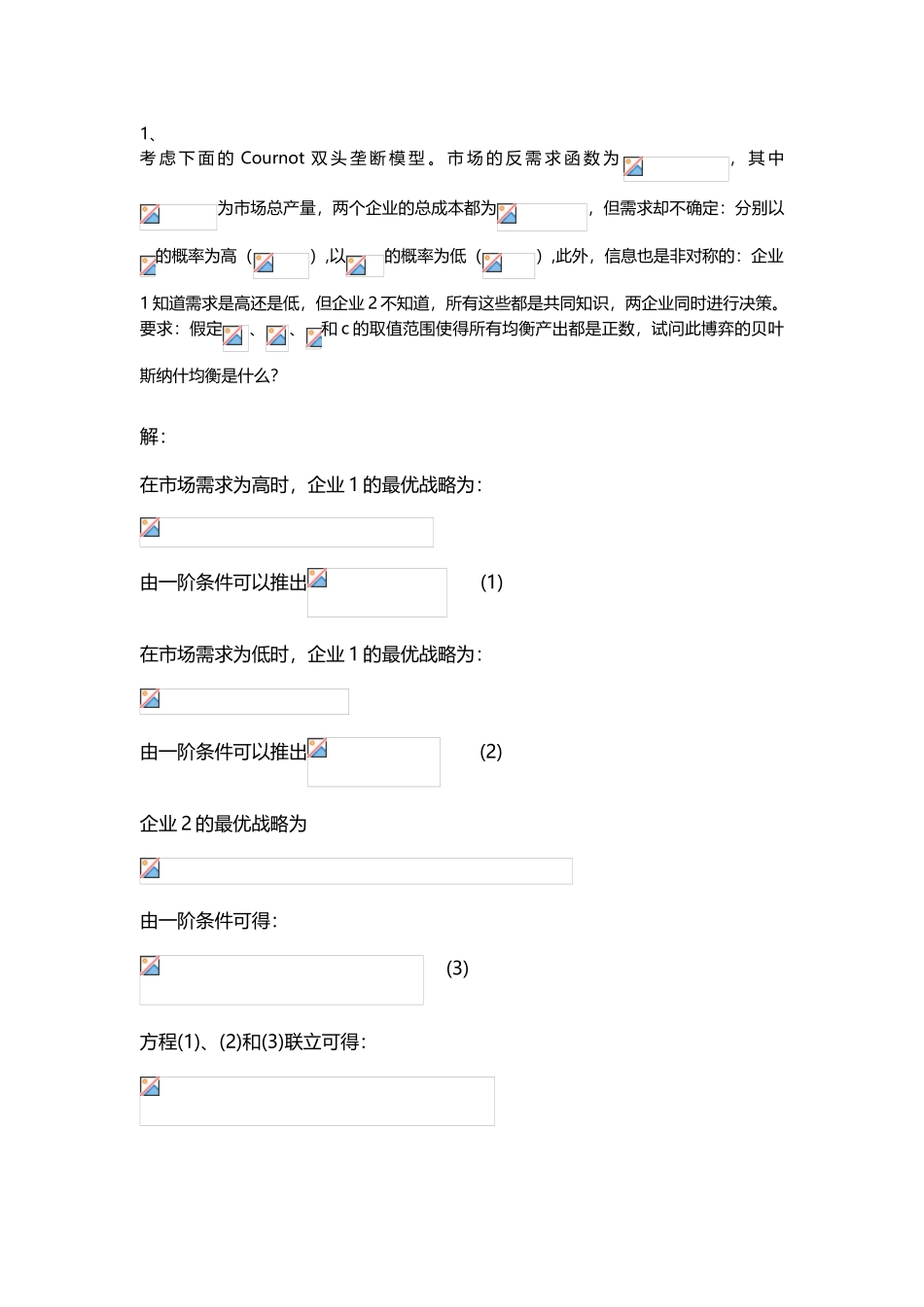
博弈考试习题(16 页)Good is good, but better carries it.精益求精,善益求善。1、考 虑 下 面 的 Cournot 双 头 垄 断 模 型 。 市 场 的 反 需 求 函 数 为, 其 中为市场总产量,两个企业的总成本都为,但需求却不确定:分别以的概率为高(),以的概率为低(),此外,信息也是非对称的:企业1 知道需求是高还是低,但企业 2 不知道,所有这些都是共同知识,两企业同时进行决策。要求:假定、、和 c 的取值范围使得所有均衡产出都是正数,试问此博弈的贝叶斯纳什均衡是什么?解:在市场需求为高时,企业 1 的最优战略为:由一阶条件可以推出 (1)在市场需求为低时,企业 1 的最优战略为:由一阶条件可以推出 (2)企业 2 的最优战略为由一阶条件可得: (3)方程(1)、(2)和(3)联立可得:由此可知,企业 1 的战略和企业 2 的战略构成贝叶斯纳什均衡。2、3、参加人 1(丈夫)和参加人 2(妻子)必须独立地决定出门时是否带伞。他们知道下雨和不下雨的可能性相同(即 50:50)。支付函数如下:假如只有一人带伞,下雨时带伞者的效用为-2.5,不带伞者(搭便车者)的效用为-3;不下雨时带伞者的效用为-1,不带伞者的效用为 0;假如两人都带伞,下雨时每人的效用为-2,不下雨时每人的效用为 1;假如两人都不带伞,下雨时每人的效用为-5,不下雨时每人的效用为 1。给出以下两种情况下的扩展式表述(博弈树)和战略式表述:(1)两人出门前都不知道是否会下雨,并且两人同时决定是否带伞(即每一方在决策时都不知道对方的决策);(2)两人出门前都不知道是否会下雨,但丈夫先决策,妻子在观察到丈夫是否带伞后才决定自己是否带伞;(3)丈夫出门前知道是否会下雨,妻子不知道,但丈夫先决策,妻子后决策;(4)同(3),但妻子先决策,丈夫后决策。解:扩展式表述:假设用 N 代表自然,H 代表丈夫,W 代表妻子。(1)(2)(3)(4)4、下面的两人博弈可以解释为两个寡头企业的价格竞争博弈,其中 p 是企业 1的价格,q 是企业 2 的价格。企业 1 的利润函数是: π1=-(p-aq+c)2+q企业 2 的利润函数是: π2=-(q-b)2+p求解: (1) 两个企业同时决策时的(纯战略)纳什均衡 (2) 企业 1 先决策时的子博弈精炼纳什均衡 (3) 企业 2 先决策时的子博弈精炼纳什均衡(4) 是否存在某些参数值(a,b,c),使得每一个企业都希望自己先决策?解: (1) 根据两个企业的利润函数,得各自的反应函数为:求解得纳什均衡...