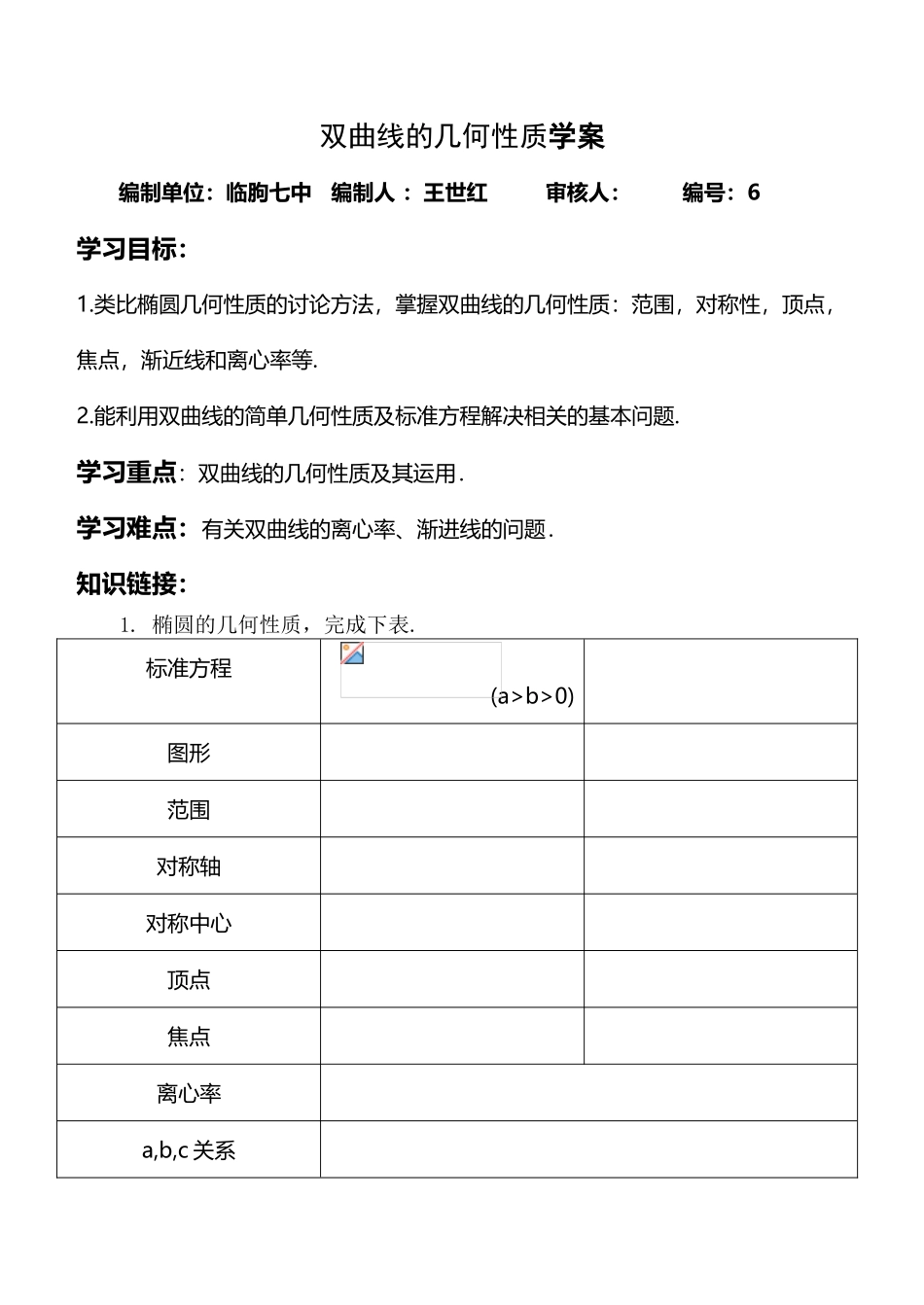
双曲线的几何性质选修 1-1(8 页)Good is good, but better carries it.精益求精,善益求善。双曲线的几何性质学案编制单位:临朐七中 编制人 :王世红 审核人: 编号:6学习目标:1.类比椭圆几何性质的讨论方法,掌握双曲线的几何性质:范围,对称性,顶点,焦点,渐近线和离心率等.2.能利用双曲线的简单几何性质及标准方程解决相关的基本问题.学习重点:双曲线的几何性质及其运用.学习难点:有关双曲线的离心率、渐进线的问题.知识链接:1. 椭圆的几何性质,完成下表.标准方程(a>b>0)图形范围对称轴对称中心顶点焦点离心率a,b,c 关系2. 双曲线的定义:3.双曲线的标准方程:学习过程一、课内探究双曲线的几何性质,完成下表标准方程(a>0,b>0)(a>0,b>0)图 形范围对称轴对称中心实虚轴顶点焦点渐近线离心率a,b,c 关系二、典例剖析例题 1:求双曲线 的实半轴长、虚半轴长、焦点坐标,离心率,渐近线方程. 跟踪训练:求下列双曲线的渐近线方程 (1)4x2-9y2=36, (2)25x2-4y2=100.例 2:跟踪训练: 例 3:双曲线型自然通风塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面,它的最小半径为 12m,上口半径为 13m,下口半径为 25m,高 55m,选择适当的坐标系,求出双曲线方程. 三、小结反思本节课我最大的收获是什么?四、当堂检测 1.求双曲线的渐近线方程是( )A.y= B. C. D.y=2.双曲线的离心率为( )A.2 B. C. 3 D.43.已知双曲线的离心率为 2,焦点是,,则双曲线方程为( )A B C. D.4.已知双曲线的焦点为、,点在双曲线上且轴,则到直线的距离为( ) (A) (B) (C) (D)五、课后巩固 1.已知双曲线的中心在原点,焦点为 F1,F2(0,),且离心率,求双曲线的标准方程及其渐近线.2.已知双曲线的中心在原点,焦点在 y 轴上,焦距为 16,离心率为,求双曲线的标准方程。3.求与双曲线共渐近线,且经过点的双曲线的标准方程及离心率. 5、双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面如图(1),它的最小半径为 12m,上口半径为 13m,下口半径为 25m,高为 55m.试选择适当的坐标系,求出双曲线的方程(各长度量精确到 1m).6.如图,设与定点的距离和它到直线 :的距离的比是常数,求点 M 的轨迹方程.六、学习后记参考答案一、课内探究二、典例剖析例 1: 跟踪训练:求下列双曲线的渐近线方程 (1)4x2-9y2=36, (2)25x2-4y2=100.(1)2x±3y=0 (2) 5x±2y=0...