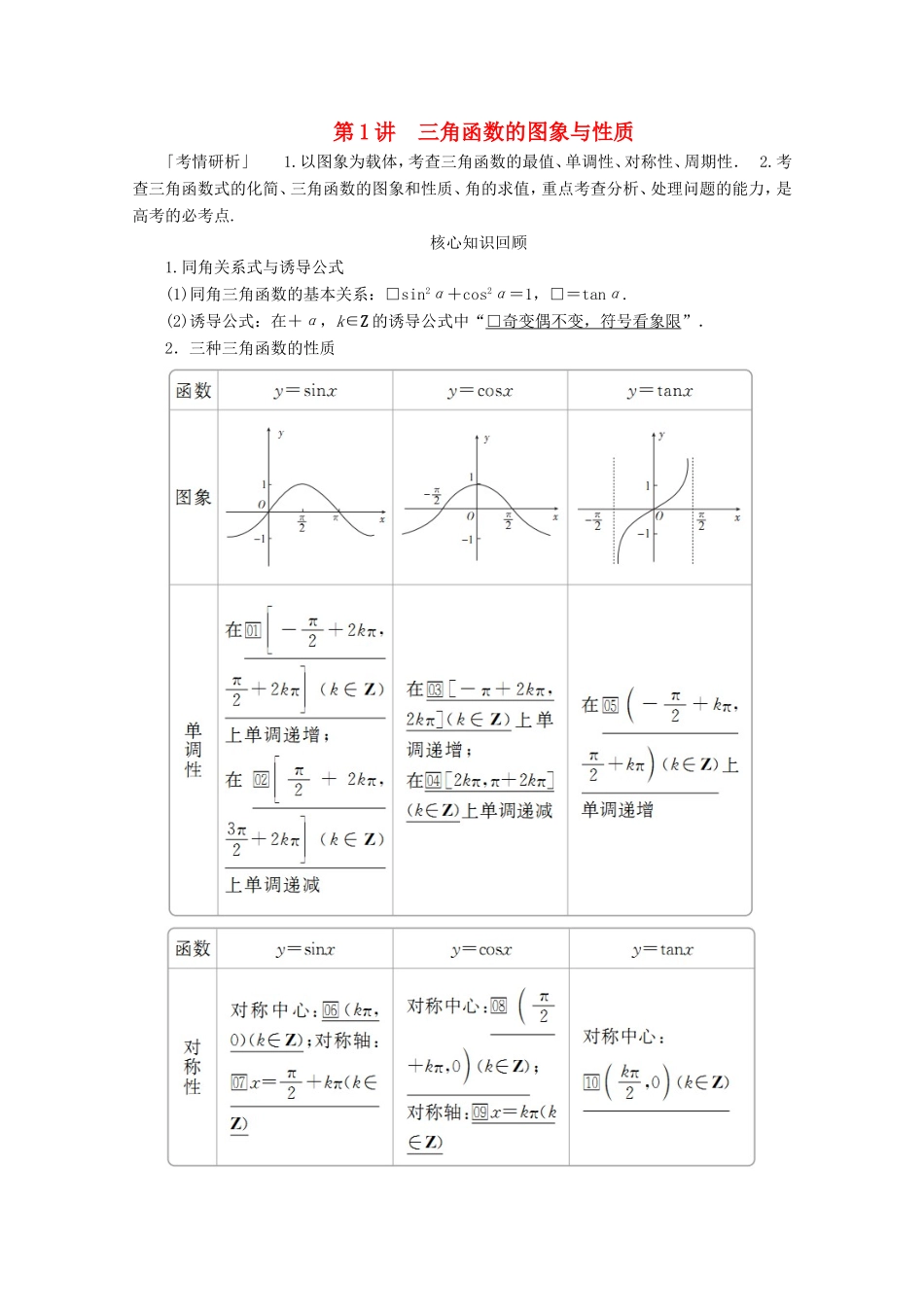
第1讲三角函数的图象与性质「考情研析」1.以图象为载体,考查三角函数的最值、单调性、对称性、周期性.2.考查三角函数式的化简、三角函数的图象和性质、角的求值,重点考查分析、处理问题的能力,是高考的必考点.核心知识回顾1.同角关系式与诱导公式(1)同角三角函数的基本关系:□sin2α+cos2α=1,□=tanα.(2)诱导公式:在+α,k∈Z的诱导公式中“□奇变偶不变,符号看象限”.2.三种三角函数的性质3.函数y=sinx的图象经变换得到y=Asin(ωx+φ)(A>0,ω>0)的图象的步骤热点考向探究考向1同角三角关系式、诱导公式例1(1)(2019·临川第一中学等九校高三3月联考)已知α∈(0,π),且cosα=-,则sintan(π+α)=()A.-B.C.-D.答案D解析sintan(π+α)=cosαtanα=sinα,因为α∈(0,π),且cosα=-,所以sinα===.故选D.(2)已知sinα-cosα=,α∈(0,π),则tanα=()A.-1B.-C.D.1答案A解析因为sinα-cosα=,所以(sinα-cosα)2=2,所以sin2α=-1.因为α∈(0,π),2α∈(0,2π),所以2α=,即α=,故tanα=-1.(3)已知α为锐角,且有2tan(π-α)-3cos+5=0,tan(π+α)+6sin(π+β)-1=0,则sinα=()A.B.C.D.-答案C解析由已知可得,-2tanα+3sinβ+5=0,①tanα-6sinβ-1=0,②①×2+②得tanα=3. α为锐角,∴sinα=.故选C.(1)利用诱导公式化简求值时,先利用公式化任意角的三角函数为锐角三角函数,其步骤:去负—脱周—化锐,特别注意函数名称和符号的确定.(2)应用公式时注意方程思想的应用:对于sinα+cosα,sinαcosα,sinα-cosα这三个式子,利用(sinα±cosα)2=1±2sinαcosα,可以知一求二.(3)关于sinα,cosα的齐次式,往往转化为关于tanα的式子求解.1.(2019·内江市高三第三次模拟)已知α∈,sinα=,则tan=()A.7B.C.-7D.-答案D解析 α∈,sinα=,∴cosα=-,∴tanα=-.∴tan==-.故选D.2.已知sin2α=,则tanα+等于()A.B.C.D.4答案A解析由sin2α=2sinαcosα=,可得sinαcosα=,所以tanα+=+==.故选A.3.如果f(tanx)=sin2x-5sinxcosx,那么f(2)=________.答案-解析 f(tanx)=sin2x-5sinxcosx==,∴f(x)=,则f(2)=-.考向2三角函数的图象及应用例2(1)(2019·永州市高三第三次模拟)将函数f(x)=sin2x+cos2x图象上各点的横坐标伸长到原来的2倍,所得函数的一个对称中心可以是()A.B.(0,0)C.D.答案A解析f(x)=sin2x+cos2x=2sin,将横坐标伸长到原来的2倍,所得函数为g(x)=2sin,令x+=kπ(k∈Z)⇒x=kπ-(k∈Z),则对称中心为,k∈Z,令k=0,则其中一个对称中心为.故选A.(2)函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的部分图象如图所示,则f(x)的单调递增区间为________.答案,k∈Z解析由函数的图象可得A=,T=-=·,解得ω=2.再根据五点作图法可知2×+φ=π,φ=,所以f(x)=sin.由-+2kπ≤2x+≤+2kπ(k∈Z),可得-+kπ≤x≤+kπ(k∈Z).1.解析式y=Asin(ωx+φ)+B的确定方法(1)A,B由最值确定,即A=,B=.(2)ω由函数周期确定,相邻两对称轴(或两对称中心)之间的距离为,对称轴与相邻对称中心之间的距离为.(3)φ由图象上的特殊点确定,利用五点作图的五个特殊点直接确定.2.三角函数图象平移问题处理策略(1)看平移要求:首先要看题目要求由哪个函数平移得到哪个函数,这是判断移动方向的关键点.(2)看移动方向:移动的方向一般记为“正向左,负向右”,看y=Asin(ωx+φ)中φ的正负和它的平移要求.(3)看移动单位:在函数y=Asin(ωx+φ)中,周期变换和相位变换都是沿x轴方向的,所以ω和φ之间有一定的关系,φ是初相,再经过ω的压缩,最后移动的单位是.1.(2019·唐山市高三第二次模拟)已知函数f(x)=sin(ω>0)的最小正周期为π,把f(x)的图象向左平移个单位后,所得函数图象的一条对称轴为()A.x=0B.x=C.x=D.x=答案B解析 函数f(x)=sin(ω>0)的最小正周期为=π,∴ω=1,f(x)=sin.若将函数f(x)的图象向左平移个单位,可得y=sin=sin的图象,令2x+=kπ+,k∈Z,求得x=+,...