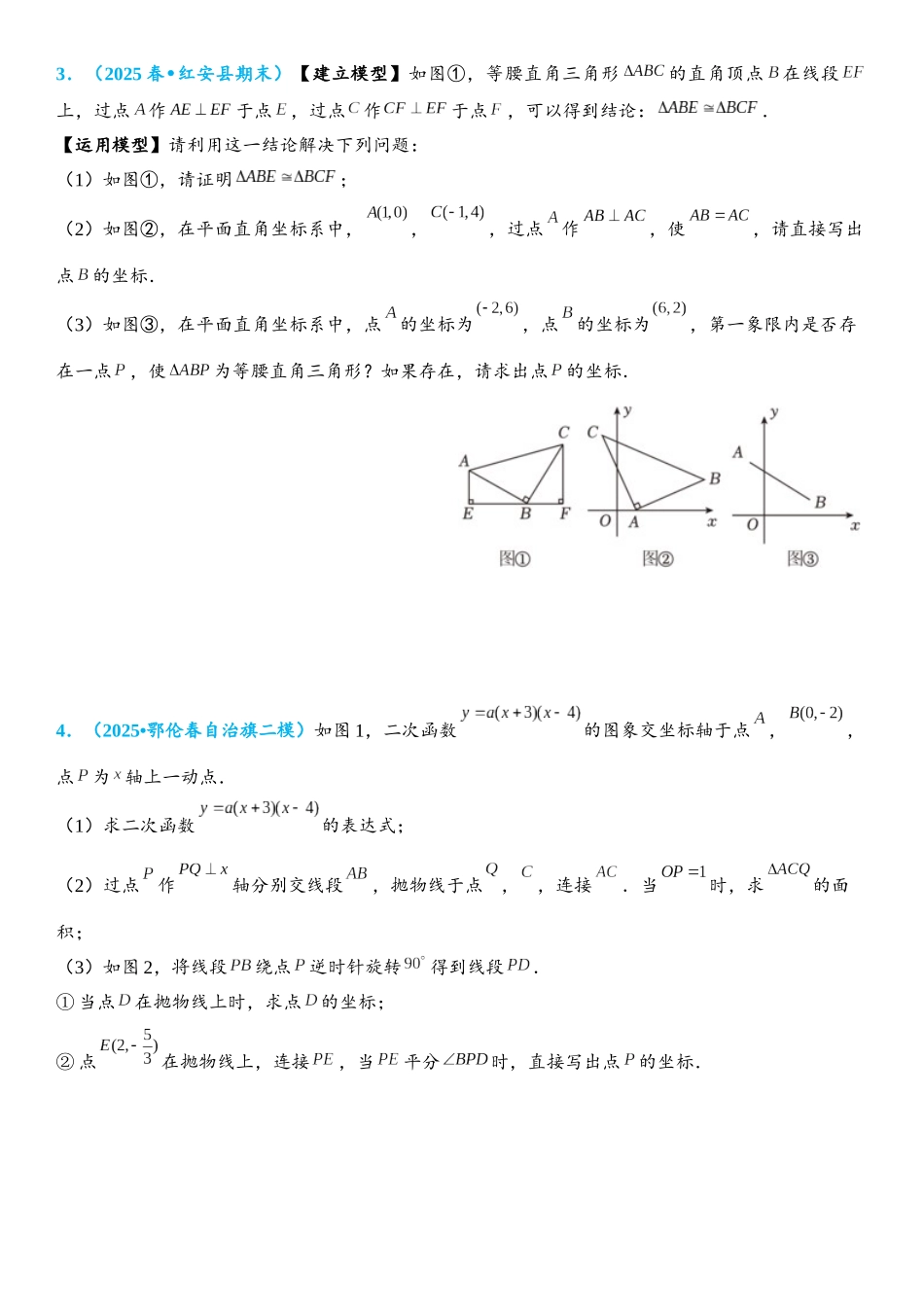
几何模型之一线三等角1.(2025 春 平阴县期末)•已知,在中,,,,三点都在直线上,.(1)如图①,若,则与的数量关系为 ,,与的数量关系为 .(2)如图②,当不垂直于时,(1)中的结论是否成立?请说明理由.(3)如图③,若只保持,,,点在线段上以的速度由点向点运动,同时,点在线段上以的速度由点向点运动,它们运动的时间为.是否存在 ,使得与全等?若存在,求出相应的 与 的值;若不存在,请说明理由.2.(2025 秋 葫芦岛期末)•在平面直角坐标系中,为等腰直角三角形,,点,点,点在第四象限.(1)如图 1,求点的坐标;(2)如图 2,若交 轴于点,交轴于点,是上一点,且,连接,求证;(3)如图 3,若点不动,点在 轴的负半轴上运动时,分别以,为直角边在第二、第三象限作等腰直角与等腰直角,其中,连接交 轴于点,问当点在 轴的负半轴上移动时,的长度是否变化?若变化,请说明理由,若不变化,请求出其长度.3.(2025 春 红安县期末)•【建立模型】如图①,等腰直角三角形的直角顶点在线段上,过点作于点,过点作于点,可以得到结论:.【运用模型】请利用这一结论解决下列问题:(1)如图①,请证明;(2)如图②,在平面直角坐标系中,,,过点作,使,请直接写出点的坐标.(3)如图③,在平面直角坐标系中,点的坐标为,点的坐标为,第一象限内是否存在一点,使为等腰直角三角形?如果存在,请求出点的坐标.4.(2025•鄂伦春自治旗二模)如图 1,二次函数的图象交坐标轴于点,,点为 轴上一动点.(1)求二次函数的表达式;(2)过点作轴分别交线段,抛物线于点,,连接.当时,求的面积;(3)如图 2,将线段绕点逆时针旋转得到线段.① 当点在抛物线上时,求点的坐标;② 点在抛物线上,连接,当平分时,直接写出点的坐标.5.(2025 春 罗庄区期末)•课本第 30 页介绍:美国总统伽菲尔德利用图 1 验证了勾股定理,直线过等腰直角三角形的直角顶点;过点作于点,过点作于点研究图形,不难发现:.(1)如图 2,在平面直角坐标系中,等腰,,,点的坐标为,点的坐标为,求点坐标;(2)如图 3,在平面直角坐标系中,直线分别与轴, 轴交于点,,将直线 绕点顺时针或逆时针旋转得到,请任选一种情况求的函数表达式;(3)如图 4,在平面直角坐标系,点,过点作轴于点,作轴于点,为线段上的一个动点,点位于第一象限(且在上方).问点,,能否构成以点为直角顶点的等腰直角...