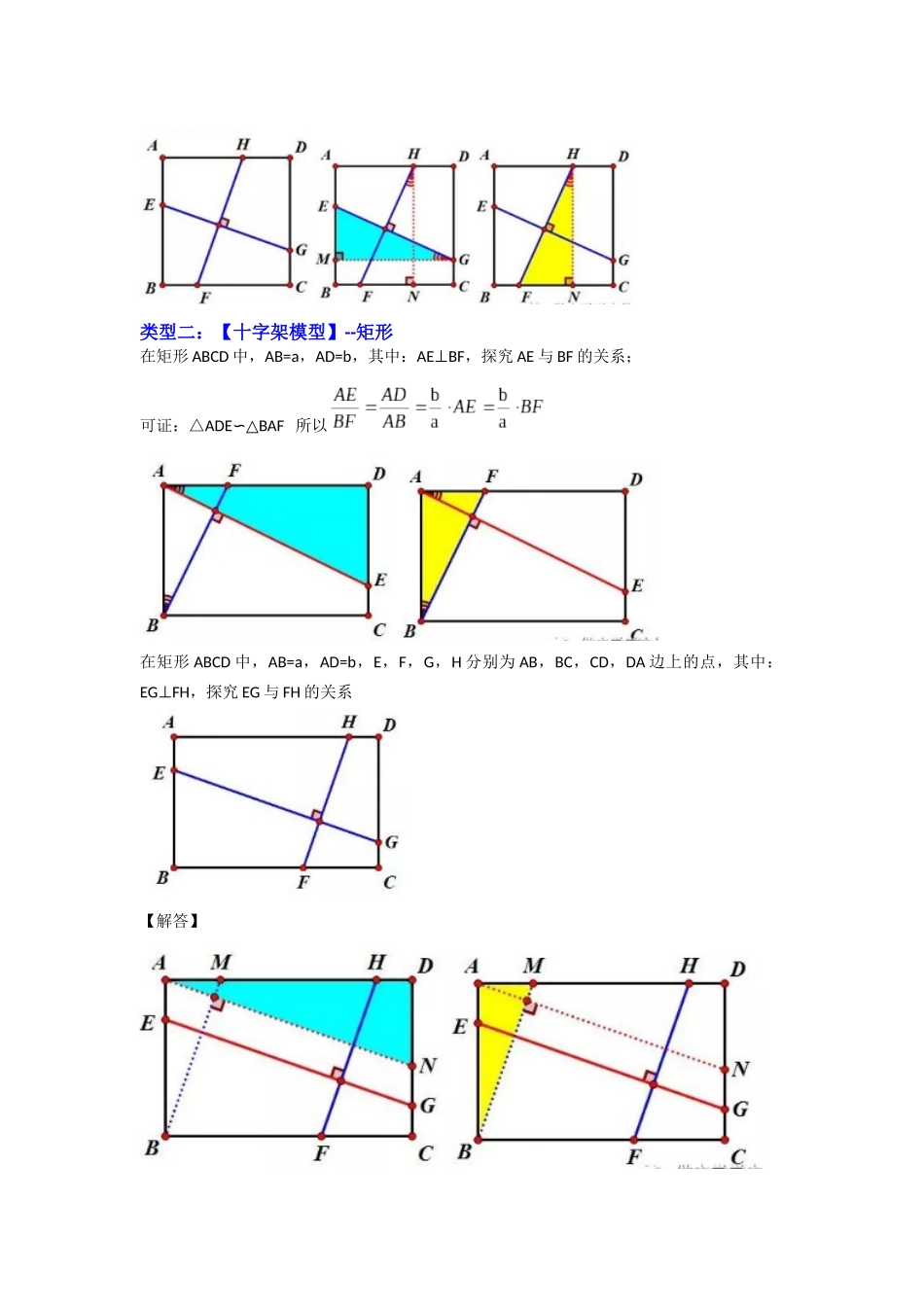
专题 08 十字模型综合应用(知识解读)【专题说明】 “十字架模型”十数学平面几何中比较重要的一个模型。常见的类型有正方形中的十字架和矩形中的十字架。围绕着这两种模型的条件之下,可以推导出一些比较实用的结论。这些结论对我们分析一些几何问题会比较大的帮助。【方法技巧】类型一:【十字架模型】--正方形第一种情况:过顶点在 正 方 形 ABCD 中 , AEBF⊥, 可 得 AE=BF , 借 助 于 同 角 的 余 角 相 等 , 证 明△BAFADE≌△(ASA)所以 AE=BF第二种情况:不过顶点在正方形 ABCD 中,E,F,G,H 分别为 AB,BC,CD,DA 边上的点,其中:EGFH⊥,可得EG=FH也可以如下证明在正方形 ABCD 中,E,F,G,H 分别 AB、BC、CD、DA 边上的点,其中:EGFH⊥,可得EG=FH类型二:【十字架模型】--矩形在矩形 ABCD 中,AB=a,AD=b,其中:AEBF⊥,探究 AE 与 BF 的关系;可证:△ADEBAF ∽△所以在矩形 ABCD 中,AB=a,AD=b,E,F,G,H 分别为 AB,BC,CD,DA 边上的点,其中:EGFH⊥,探究 EG 与 FH 的关系【解答】可证:△ADNBAM∽△∴∴但是只有垂直的条件,点的位置发生变化,那么可以证明出相似三角形,但是线段之间的关系不在成立在矩形 ABCD 中,AB=a,AD=b,其中 EGFH⊥,探究 EG 与 FH 的关系可证△EOHGOF∽△【典例分析】【典例 1-1】基本模型如图,在正方形 ABCD 中,点 E、F 分别在 AD,DC 边上,且 AF⊥BE.结论:①△ABE△DAF; ② AF=BE;请证明【基本模型】中的结论.求证:①△ABE≌△DAF;② AF=BE.自主探究:若将已知条件 AF⊥BE 改为 AF=BE,是否可以得到 AF⊥BE?进而是否可以探究 AF 与 BE 交点的轨迹?【典例 1-2】模型演变①如图①,在正方形 ABCD 中,点 E,F,G 分别在 DC,AD,BC 边上,且 AE⊥GF.结论:AE=GF模型演变②如图②,在正方形 ABCD 中,点 E,F,G,H 分别在 AB,DC,BC,AD 边上,且EF⊥GH.结论:EF=GH请证明【模型演变②】的结论,求证:EF=GH.自主探究:在【模型演变①】和【模型演变②】中,若将已知条件中两线段垂直与结论中两线段相等互换,判断结论是否还成立?请选择其中一个图形进行证明.【典例 2-1】模型演变③如图,在矩形 ABCD 中,点 E 在 AD 边上,且 CE⊥BD.结论:△DCE∽△ADB请证明【模型演变③】的结论.求证:△DCE∽△ADB.【典例 2-2】模型演变④如图,在矩形 ...