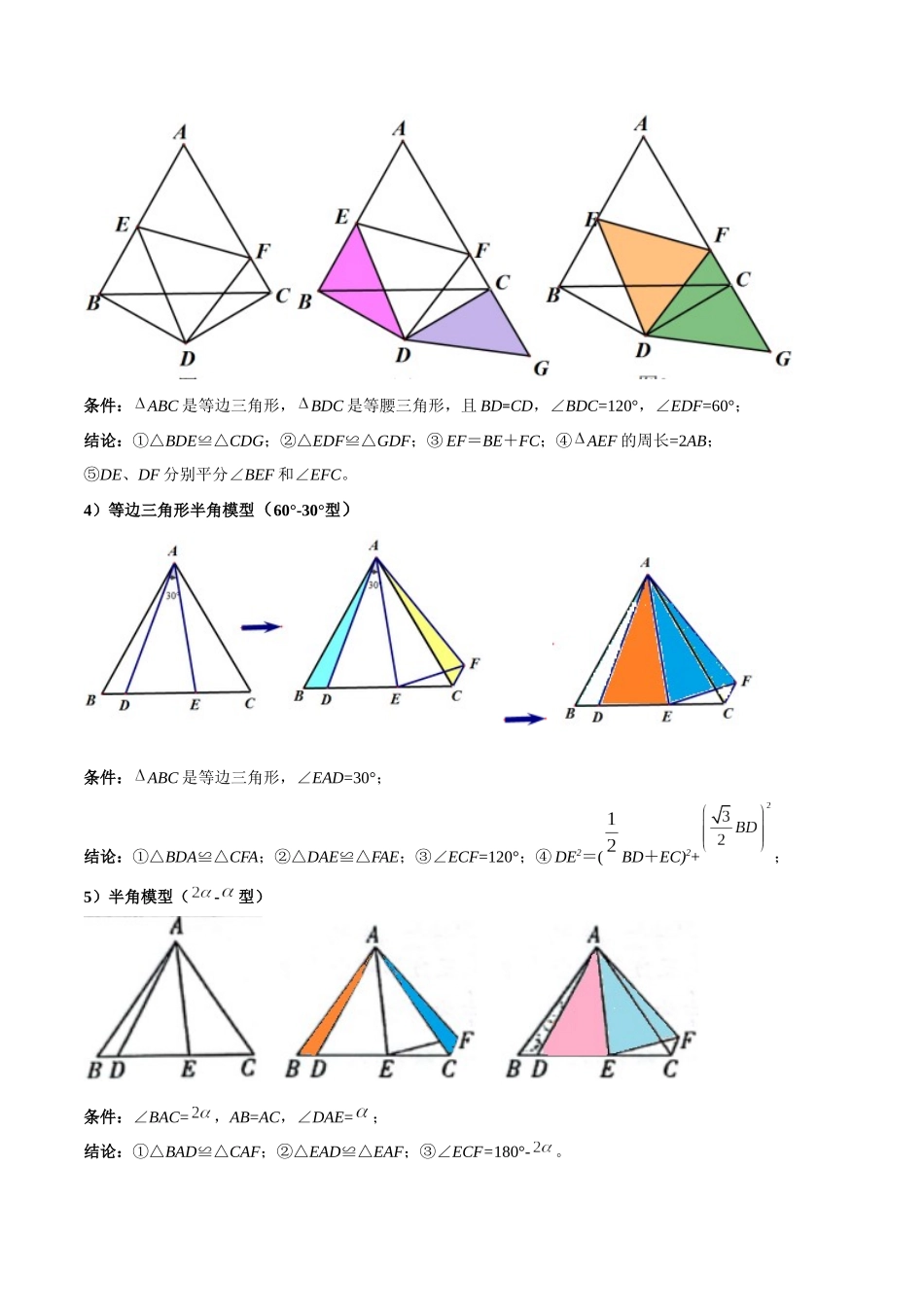
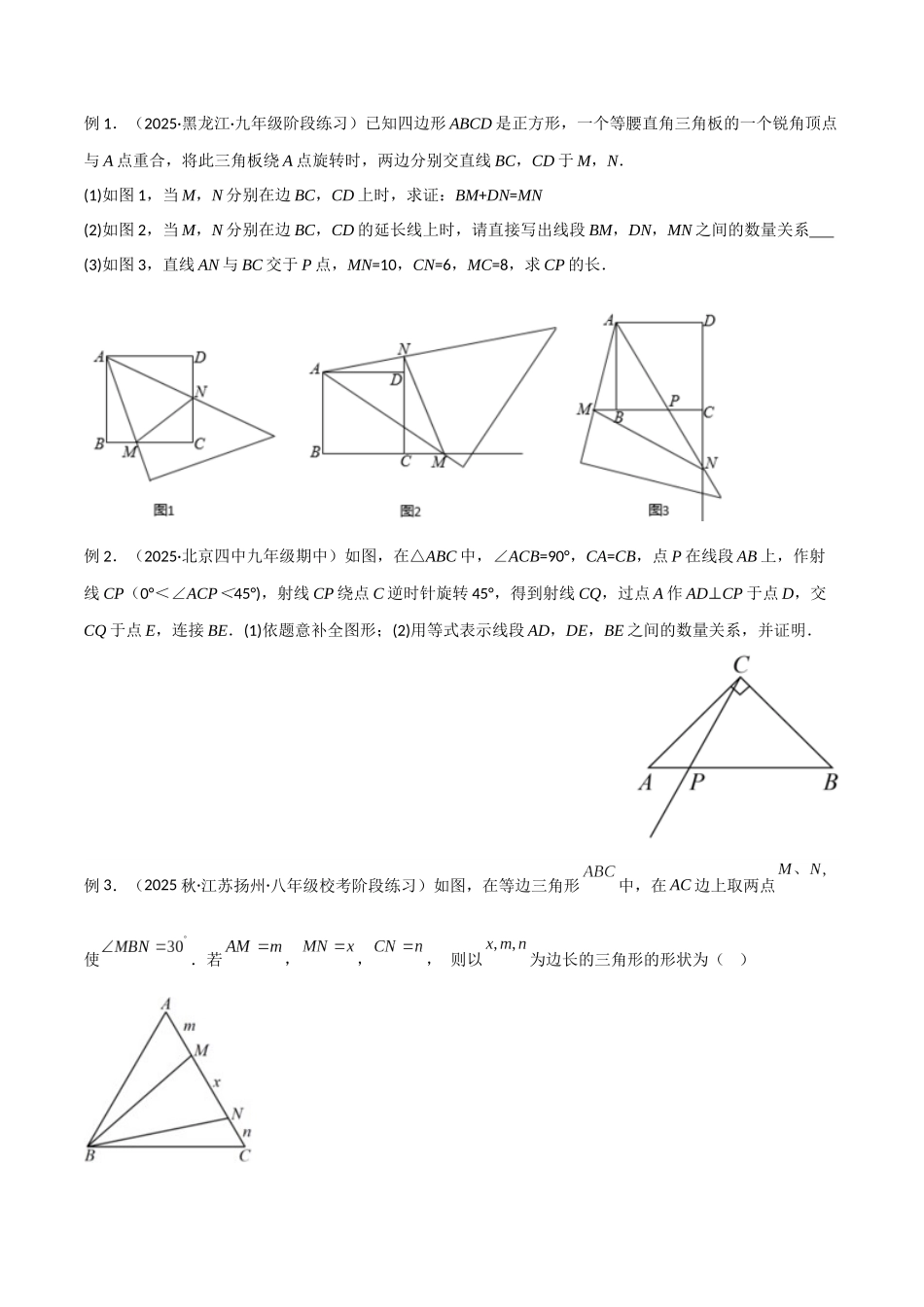
专题 16 全等与相似模型-半角模型全等三角形与相似三角形在中考数学几何模块中占据着重要地位。相似三角形与其它知识点结合以综合题的形式呈现,其变化很多,难度大,是中考的常考题型。如果大家平时注重解题方法,熟练掌握基本解题模型,再遇到该类问题就信心更足了。本专题就半角模型进行梳理及对应试题分析,方便掌握。模型 1.半角模型半角模型概念:过多边形一个顶点作两条射线,使这两条射线夹角等于该顶角一半。思想方法:通过旋转(或截长补短)构造全等三角形,实现线段的转化。解题思路一般是将半角两边的三角形通过旋转到一边合并成新的三角形,从而进行等量代换,然后证明与半角形成的三角形全等,再通过全等的性质得到线段之间的数量关系。半角模型(题中出现角度之间的半角关系)利用旋转——证全等——得到相关结论。【模型展示】1)正方形半角模型条件:四边形 ABCD 是正方形,∠ECF=45°;结论:①△BCE≌△DCG;②△CEF≌△CGF;③ EF=BE+DF;④AEF 的周长=2AB;⑤CE、CF 分别平分∠BEF 和∠EFD。2)等腰直角三角形半角模型条件:ABC 是等腰直角三角形,∠DAE=45°;结论:①△BAD≌△CAG;②△DAE≌△GAE;③∠ECG=90°;④ DE2=BD2+EC2;3)等边三角形半角模型(120°-60°型)条件:ABC 是等边三角形,BDC 是等腰三角形,且 BD=CD,∠BDC=120°,∠EDF=60°;结论:①△BDE≌△CDG;②△EDF≌△GDF;③ EF=BE+FC;④AEF 的周长=2AB;⑤DE、DF 分别平分∠BEF 和∠EFC。4)等边三角形半角模型(60°-30°型)条件:ABC 是等边三角形,∠EAD=30°;结论:①△BDA≌△CFA;②△DAE≌△FAE;③∠ECF=120°;④ DE2=(BD+EC)2+;5)半角模型(-型) 条件:∠BAC=,AB=AC,∠DAE=;结论:①△BAD≌△CAF;②△EAD≌△EAF;③∠ECF=180°-。例 1.(2025·黑龙江·九年级阶段练习)已知四边形 ABCD 是正方形,一个等腰直角三角板的一个锐角顶点与 A 点重合,将此三角板绕 A 点旋转时,两边分别交直线 BC,CD 于 M,N.(1)如图 1,当 M,N 分别在边 BC,CD 上时,求证:BM+DN=MN(2)如图 2,当 M,N 分别在边 BC,CD 的延长线上时,请直接写出线段 BM,DN,MN 之间的数量关系 (3)如图 3,直线 AN 与 BC 交于 P 点,MN=10,CN=6,MC=8,求 CP 的长.例 2.(2025·北京四中九年级期中)如图,在△ABC 中,∠ACB=90°,CA=CB,点 P 在线段 AB 上,作射线 CP(0°<∠A...