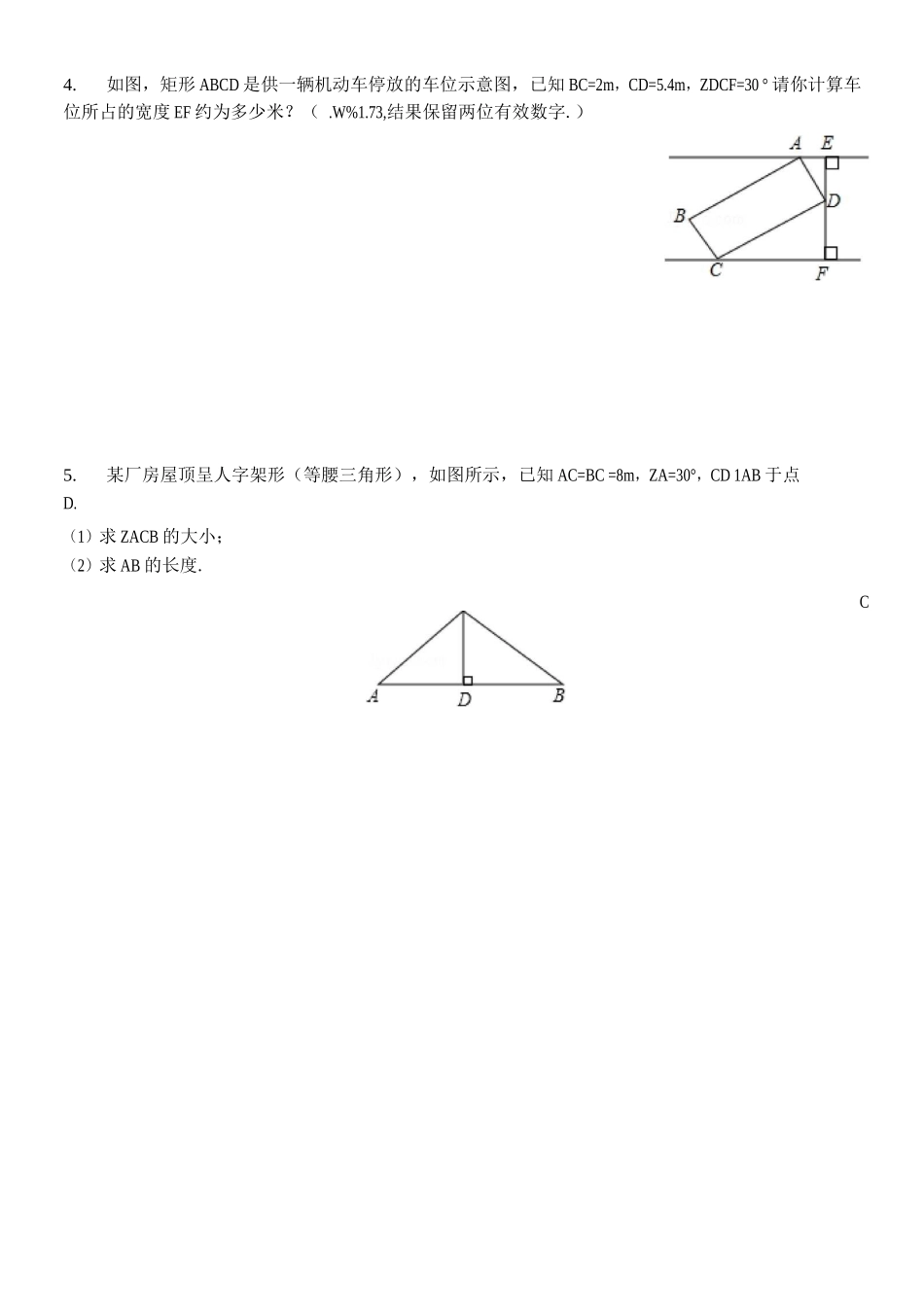
解直角三角形的应用复习1.校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设 计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点 C,再在笔直的车道 l 上确定 点 D,使 CD 与 l 垂直,测得 CD 的长等于 21 米,在 l 上点 D 的同侧取点 A、B,使 ZCAD=30 °, ZCBD=60 °.__(1)求 AB 的长(精确到 0.1 米,参考数据:2=1.73,克=1.41);(2)已知本路段对校车限速为 40 千米/小时,若测得某辆校车从 A 到 B 用时 2 秒,这辆校车是否 超速?说明理由.2.如图,公路的两边 CF,DE 互相平行,线段 CD 为人行横道,公路两侧的 A,B 两点分别表示 车站和超市.CD 与 AB 所在直线互相平行,且都与公路的两边垂直,公路宽 20 米,A,B 相距 62 米,NA=67 °,NB=37 °.(1)求 CD 与 AB 之间的距离;(2)某人从车站 A 出发接横穿公路多走多少米.(参考数据:sin6°墓,133.2025 年 3 月,某煤矿发生瓦斯爆炸,该地救援队立即赶赴现场进行救援,救援队利用生命探测 仪在地面 A、B 两个探测点探测到 C 处有生命迹象.已知 A、B 两点相距 4 米,探测线与地面的 夹角分别是 30°和 45°,试确定生命所在点 C 的深度.(精确到 0.1 米,参考数据: ,另刁.41, ,§#1.73)沿折线 A 一 D — C 一 B 去超市 B.求他沿折线 A 一 D — C 一 B 到达超市比直cos67° 直, tan67 基, SM375 直,1355,cos37° 壹54.如图,矩形 ABCD 是供一辆机动车停放的车位示意图,已知 BC=2m,CD=5.4m,ZDCF=30 ° 请你计算车位所占的宽度 EF 约为多少米?( .W%1.73,结果保留两位有效数字.)5.某厂房屋顶呈人字架形(等腰三角形),如图所示,已知 AC=BC =8m,ZA=30°,CD 1AB 于点D.(1)求 ZACB 的大小;(2)求 AB 的长度.C6.如图,某风景区内有一古塔 AB,在塔的一侧有一建筑物,当光线与水平面的夹角是 30°时,塔 在建筑物的墙上留下了高为 3 米的影子 CD ;而当光线与地面的夹角是 45°时,塔尖 A 在地面上的 影子 E 与建筑物的距离 EC 为 15 米(B、E、C 在一条直线上),求塔 AB 的高度(结果保留根号).A7.如图,在梯形 ABCD 中,AD IIBC,AD =3, DC =5, AB =4 .WNB=45。.动点 M 从 B 点出发沿 线段 BC 以每秒 2 个单位长度的速度向终点 C 运动;动点 N 同时从 C 点出发...