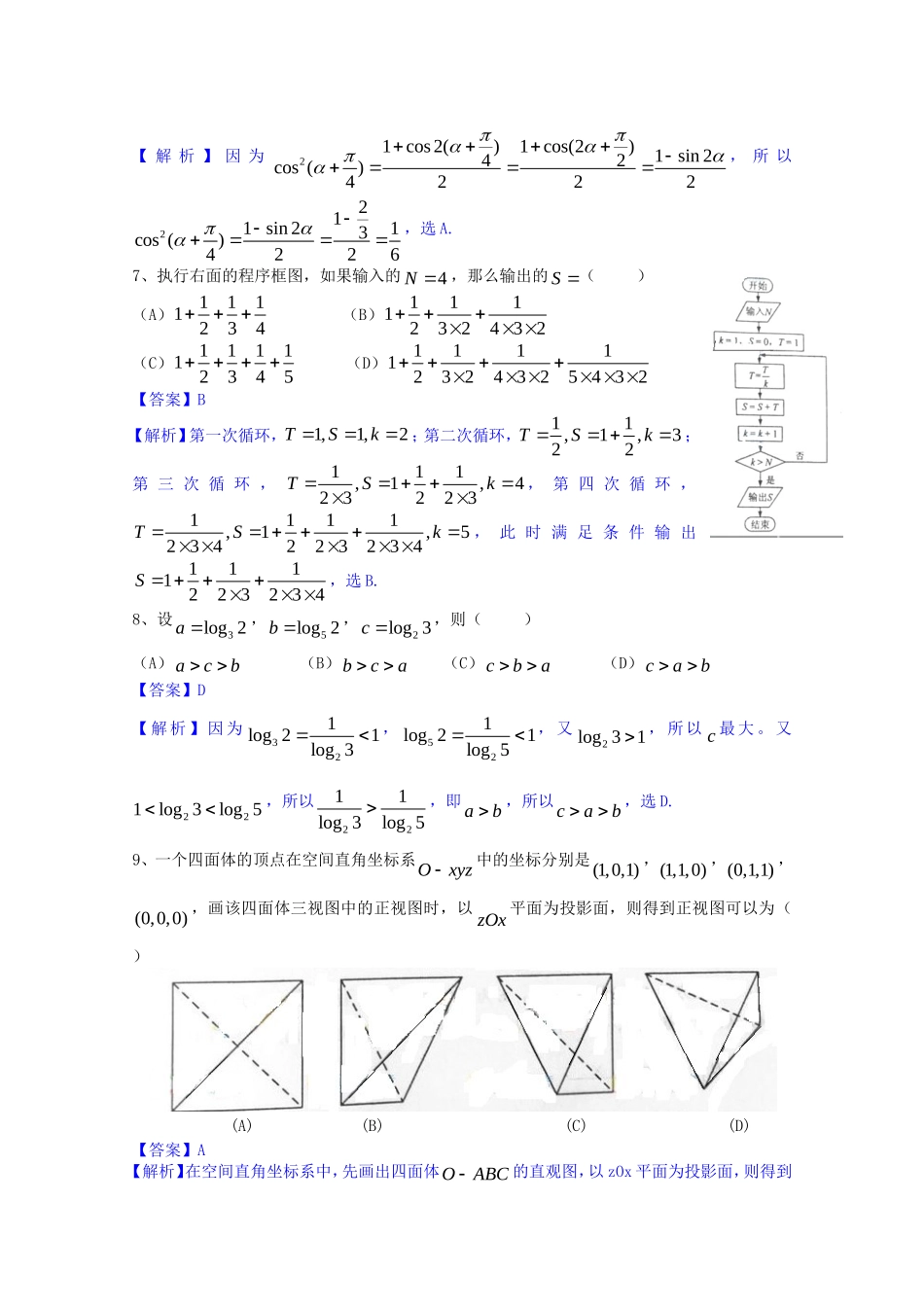
普通高等学校招生全国统一考试(新课标Ⅱ卷)数学(文科)1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。答卷前考生将自己的姓名\准考证号填写在本试卷和答题卡相应位置。2.回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号标黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。3.答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。4.考试结束,将试题卷和答题卡一并交回。第Ⅰ卷(选择题共50分)一、选择题:本大题共10小题。每小题5分,共50分。在每个小题给出的四个选项中,只有一项是符合题目要求的。1、已知集合{|31}Mxx,{3,2,1,0,1}N,则MN()(A){2,1,0,1}(B){3,2,1,0}(C){2,1,0}(D){3,2,1}【答案】C【解析】因为{31}Mxx,{3,2,1,0,1}N,所以MN{2,1,0},选C.2、21i()(A)22(B)2(C)2(D)1【答案】C【解析】22(1)2(1)11(1)(1)2iiiiii,所以221i,选C.3、设,xy满足约束条件10,10,3,xyxyx,则23zxy的最小值是()(A)7(B)6(C)5(D)3【答案】B【解析】由z=2x-3y得3y=2x-z,即233zyx。作出可行域如图,平移直线233zyx,由图象可知当直线233zyx经过点B时,直线233zyx的截距最大,此时z取得最小值,由103xyx得34xy,即(3,4)B,代入直线z=2x-3y得32346z,选B.4、ABC的内角,,ABC的对边分别为,,abc,已知2b,6B,4C,则ABC的面积为()(A)232(B)31(C)232(D)31【答案】B【解析】因为,64BC,所以712A.由正弦定理得sinsin64bc,解得22c。所以三角形的面积为117sin222sin2212bcA.因为73221231sinsin()()12342222222,所以1231sin22()312222bcA,选B.5、设椭圆2222:1xyCab(0)ab的左、右焦点分别为12,FF,P是C上的点,22,1230PFF,则C的离心率为()(A)36(B)13(C)12(D)33【答案】D【解析】因为21212,30PFFFPFF,所以2123432tan30,33PFccPFc。又126323PFPFca,所以1333ca,即椭圆的离心率为33,选D.6、已知2sin23,则2cos()4()(A)16(B)13(C)12(D)23【答案】A【解析】因为21cos2()1cos(2)1sin242cos()4222,所以2211sin213cos()4226,选A.7、执行右面的程序框图,如果输入的4N,那么输出的S()(A)1111234(B)1111232432(C)111112345(D)111112324325432【答案】B【解析】第一次循环,1,1,2TSk;第二次循环,11,1,322TSk;第三次循环,111,1,423223TSk,第四次循环,1111,1,5234223234TSk,此时满足条件输出1111223234S,选B.8、设3log2a,5log2b,2log3c,则()(A)acb(B)bca(C)cba(D)cab【答案】D【解析】因为321log21log3,521log21log5,又2log31,所以c最大。又221log3log5,所以2211log3log5,即ab,所以cab,选D.9、一个四面体的顶点在空间直角坐标系Oxyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx平面为投影面,则得到正视图可以为()(A)(B)(C)(D)【答案】A【解析】在空间直角坐标系中,先画出四面体OABC的直观图,以zOx平面为投影面,则得到正视图(坐标系中红色部分),所以选A.10、设抛物线2:4Cyx的焦点为F,直线l过F且与C交于A,B两点。若||3||AFBF,则l的方程为()(A)1yx或!yx(B)3(1)3yx或3(1)3yx(C)3(1)yx或3(1)yx(D)2(1)2yx或2(1)2yx【答案】C【解析】抛物线y2=4x的焦点坐标为(1,0),准线方程为x=-1,设A(x1,y1),B(x2,y2),则因为|AF|=3|BF|,所以x1+1=3(x2+1),所以x1=3x2+2因为|y1|=...