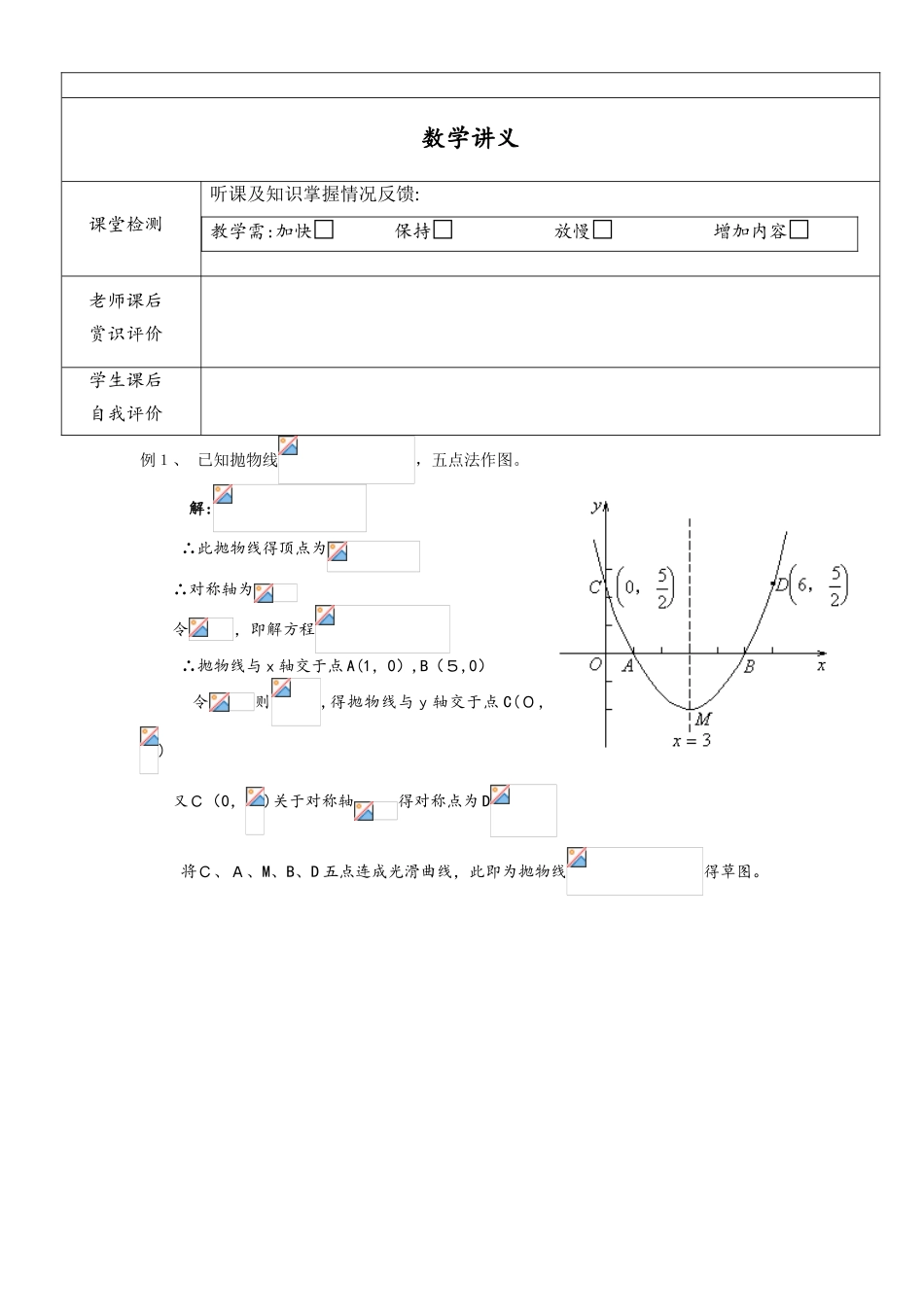
个 性 化 辅 导 教 案科 目 数学 授课老师学生姓名年 级课 题教学目标重 点 重点掌握二次函数定义、解析式、图象及其性质难 点难点是配方法求顶点坐标,只要坚持配完后看看与原二次函数是否相等即可教学过程(内容):1、 掌握二次函数得概念,形如得函数,叫做二次函数,定义域。 特别地,时,是二次函数特例。 2、 能由实际问题确定函数解析式和自变量取值范围,明确它有三个待定系数a,b,c,,需三个相等关系,才可解。 3、 二次函数解析式有三种: (1) 一般式 (2) 顶点式; 顶点 (3) 双根式;是图象与 x 轴交点坐标。 4、 二次函数图象:抛物线 分布象限,可能在两个象限(1),三个象限(2),四个象限(3)。 5、 抛物线与抛物线形状、大小相同,只有位置不同。 6、 描点法画抛物线了解开口、顶点、对称轴、最值。 (1)a 决定开口: 开口向上,开口向下。 表示开口宽窄,越大开口越窄。 (2)顶点,当时,y 有最值为。 (3)对称轴 (4)与 y 轴交点(0,c),有且仅有一个 (5)与x轴交点 A(),B(),令则。 ①△>0,有,两交点 A、B。 ②△=0,有,一个交点。 ③△<0,没有实数与x轴无交点。 7、 配方可得 向右()或向左()平移个单位,得到,再向上向下平移个单位,便得,即 。 8、 五点法作抛物线 (1)找顶点,画对称轴。 (2)找图象上关于直线对称得四个点(如与坐标轴得交点等)。 (3)把上述五个点连成光滑曲线。 9、 掌握二次函数与一元二次方程、一元二次不等式得关系。判别式二次函数()无实根一元二次或不等于得实数全体实数不等式空集空集数学讲义课堂检测听课及知识掌握情况反馈:教学需:加快□ 保持□ 放慢□ 增加内容□老师课后赏识评价学生课后自我评价例1、 已知抛物线,五点法作图。 解: ∴此抛物线得顶点为 ∴对称轴为 令,即解方程 ∴抛物线与x轴交于点 A(1,0),B(5,0) 令则,得抛物线与y轴交于点 C(0,) 又C(0,)关于对称轴得对称点为 D 将C、A、M、B、D 五点连成光滑曲线,此即为抛物线得草图。 例 2、 已知抛物线如图,试确定: (1)及得符号; (2)与得符号。 解:(1)由图象知抛物线开口向下,对称轴在 y 轴左侧,过 A(1,0)与y轴交于 B(0,c),在 x 轴上方 抛物线与x轴有两交点 (2) 抛物线过 A(1,0) 例 3、 求二次函数解析式: (1)抛物线过(0,2),(1,1),(3,5); (2)顶点M(-1,2),且过 N(2,1)...