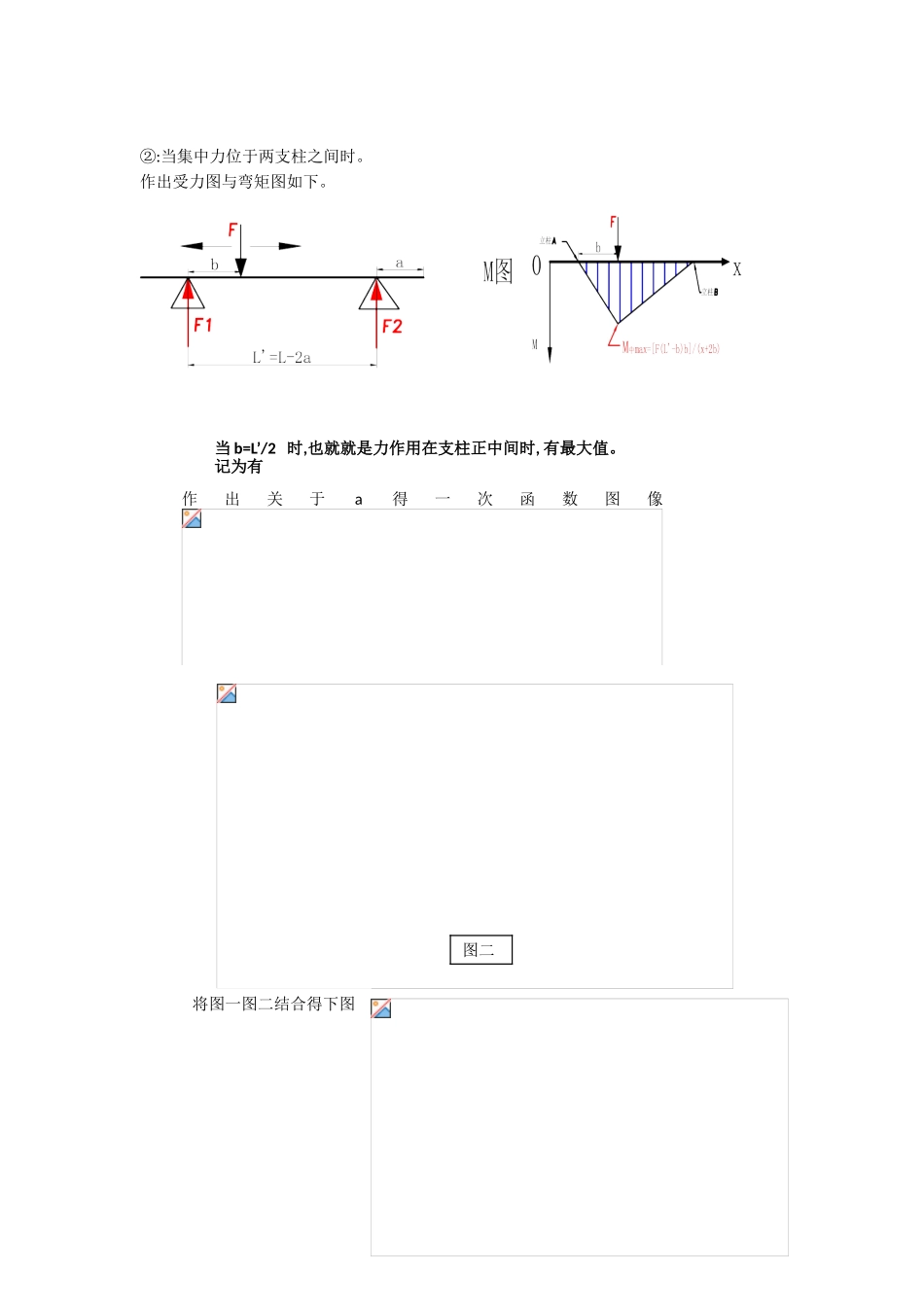
双杠就是体操运动得常用器械,其设计应该符合力学原理。为方便设计,假设只考虑运动员作用在双杠上铅垂向下得力,且双杠得横杆为等截面直杆。请分析: (1)本问题与力学中得什么问题有关系? (2)建立学模型。 (3)确定立横杆得立柱得位置,用 a 与 l 得比值表示。 假定运动员在双杠上做动作时,在每根横杆上只有一个力得作用点力得作用线垂直于横杆,而且力得大小与作用点得位置无关。 解答:(1):本题设计材料力学中弯曲内力得问题。以及梁得合理设计。 (2):建立力学模型由于横杆受力处于铅垂方向,两根横杆互不影响,取其中一根讨论。将竖杆简化为铰链支座。 建立力学模型为:受一集中力得两端外伸梁,。如图:(3):确定立横杆得立柱得位置,用 a 与 l 得比值表示由题意得,欲确定立柱得最佳位置,则应使结构所受得最大应力最小。因外力 F恒定所以竖杆所受正应力最大值恒定。欲确定竖杆最佳位置应从横杆受力情况分析。再由梁得应力公式: 由于双杠横杆为等截面圆杆,则恒定。仅由确定。下面计算横梁得最大弯矩①:当集中力位于支柱外侧时(下图),很明显力在杆端点处支座处有弯矩最大值。画出梁得弯矩图如下、记 A 点处弯矩最大值为,有作出关于 a 得一次函数图像图一②:当集中力位于两支柱之间时。作出受力图与弯矩图如下。当 b=L’/2 时,也就就是力作用在支柱正中间时, 有最大值。记为有 作出关于a得一次函数图像图二将图一图二结合得下图由图得当M max1=Mm ax 2 时,Mma x 1、Mmax 2共同达到最大值,M ma x 有最小值、此时解得:也就就是说,双杠外伸端得长度为双杠总长度得六分之一时,竖杆得位置最合理