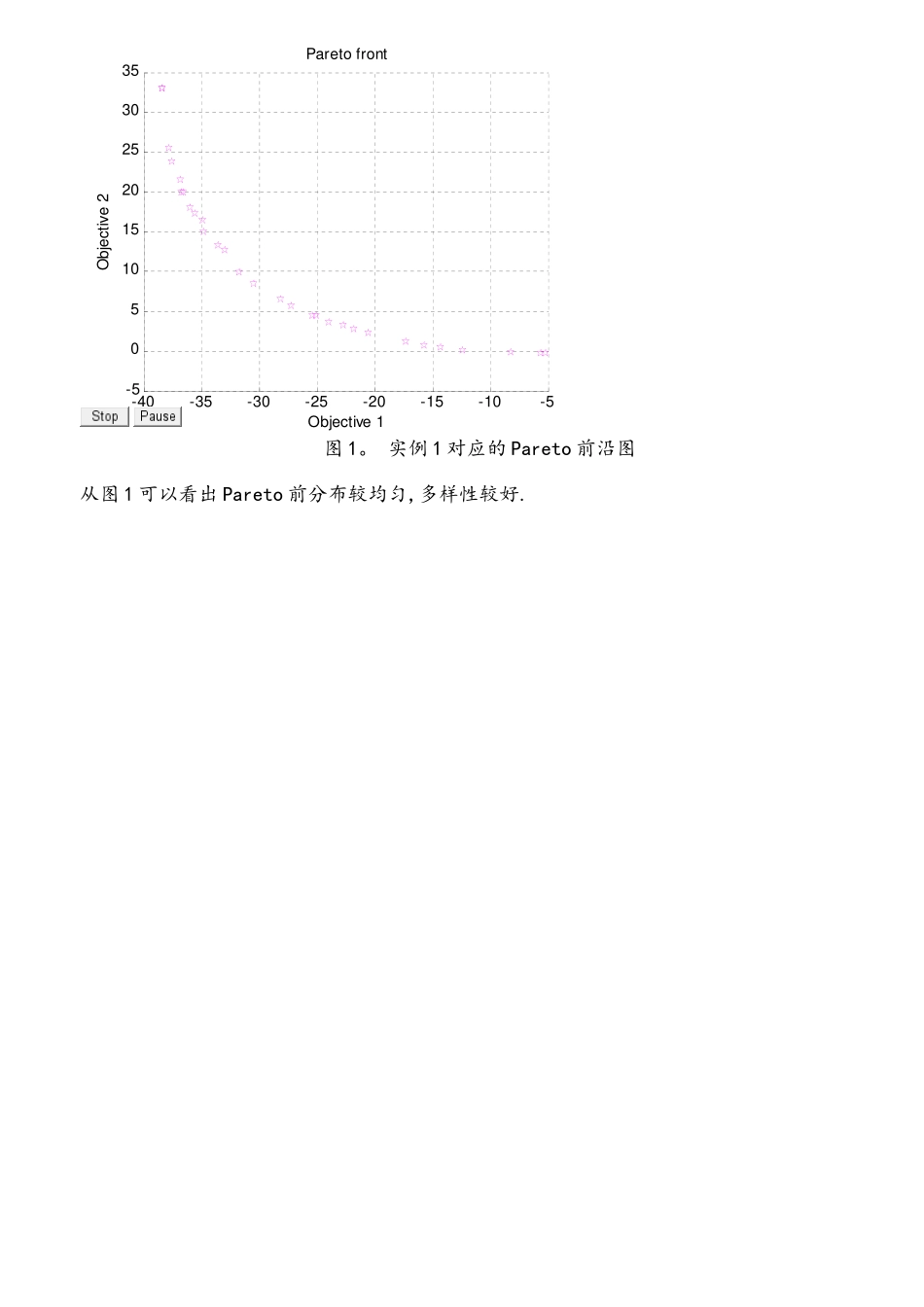
NSGA-II 算法实例目前的多目标优化算法有很多, Kalyanmoy Deb 的带精英策略的快速非支配排序遗传算法(NSGA-II) 无疑是其中应用最为广泛也是最为成功的一种。本文用的算法是 MATLAB 自带的函数gamultiobj,该函数是基于 NSGA—II 改进的一种多目标优化算法。一、数值例子多目标优化问题二、Matlab 文件1. 适应值函数 m 文件:function y=f(x)y(1)=x(1)^4-10*x(1)^2+x(1)*x(2)+x(2)^4-x(1)^2*x(2)^2;y(2)=x(2)^4—x(1)^2*x(2)^2+x(1)^4+x(1)*x(2);2. 调用 gamultiobj 函数,及参数设置:clearclcfitnessfcn=@f; %适应度函数句柄nvars=2; %变量个数lb=[—5,—5]; %下限ub=[5,5]; %上限A=[];b=[]; %线性不等式约束Aeq=[];beq=[]; %线性等式约束options=gaoptimset(’paretoFraction',0。3,'populationsize',100,'generations’,200,’stallGenLimit’,200,’TolFun’,1e-100,’PlotFcns',@gaplotpareto);% 最优个体系数 paretoFraction 为 0.3;种群大小 populationsize 为 100,最大进化代数 generations 为 200,% 停止代数 stallGenLimit 为 200, 适应度函数偏差 TolFun 设为 1e-100,函数gaplotpareto:绘制 Pareto 前端[x,fval]=gamultiobj(fitnessfcn,nvars,A,b,Aeq,beq,lb,ub,options)3。 计算结果-40-35-30-25-20-15-10-5-505101520253035Objective 1Objective 2Pareto front图 1。 实例 1 对应的 Pareto 前沿图从图 1 可以看出 Pareto 前分布较均匀,多样性较好.