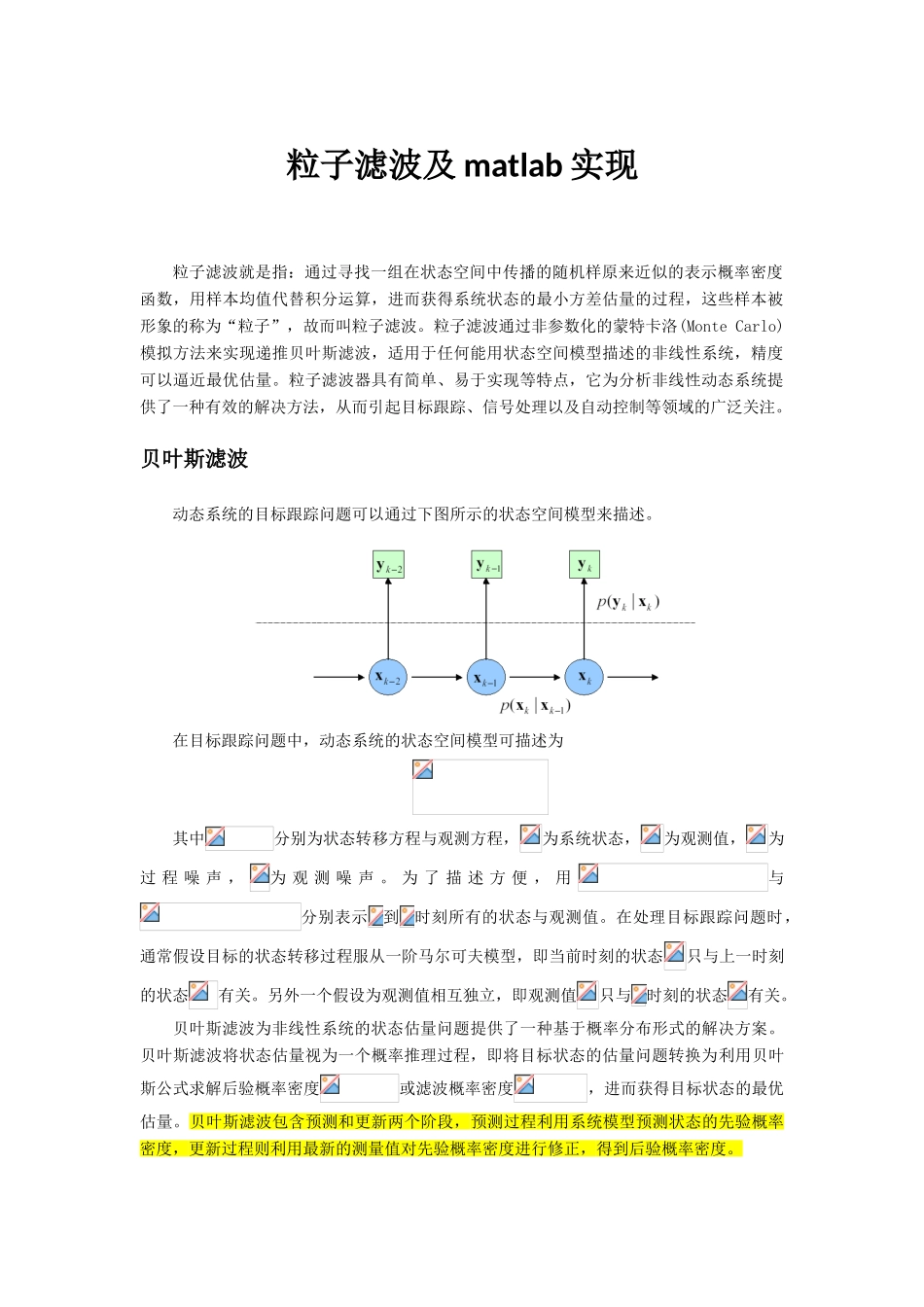
粒子滤波及 matlab 实现粒子滤波就是指:通过寻找一组在状态空间中传播的随机样原来近似的表示概率密度函数,用样本均值代替积分运算,进而获得系统状态的最小方差估量的过程,这些样本被形象的称为“粒子”,故而叫粒子滤波。粒子滤波通过非参数化的蒙特卡洛(Monte Carlo)模拟方法来实现递推贝叶斯滤波,适用于任何能用状态空间模型描述的非线性系统,精度可以逼近最优估量。粒子滤波器具有简单、易于实现等特点,它为分析非线性动态系统提供了一种有效的解决方法,从而引起目标跟踪、信号处理以及自动控制等领域的广泛关注。贝叶斯滤波动态系统的目标跟踪问题可以通过下图所示的状态空间模型来描述。在目标跟踪问题中,动态系统的状态空间模型可描述为其中分别为状态转移方程与观测方程,为系统状态,为观测值,为过 程 噪 声 ,为 观 测 噪 声 。 为 了 描 述 方 便 , 用与分别表示到时刻所有的状态与观测值。在处理目标跟踪问题时,通常假设目标的状态转移过程服从一阶马尔可夫模型,即当前时刻的状态只与上一时刻的状态有关。另外一个假设为观测值相互独立,即观测值只与时刻的状态有关。贝叶斯滤波为非线性系统的状态估量问题提供了一种基于概率分布形式的解决方案。贝叶斯滤波将状态估量视为一个概率推理过程,即将目标状态的估量问题转换为利用贝叶斯公式求解后验概率密度或滤波概率密度,进而获得目标状态的最优估量。贝叶斯滤波包含预测和更新两个阶段,预测过程利用系统模型预测状态的先验概率密度,更新过程则利用最新的测量值对先验概率密度进行修正,得到后验概率密度。假设已知时刻的概率密度函数为,贝叶斯滤波的具体过程如下:(1) 预测过程,由得到: 当给定时,状态与相互独立,因此上式两端对积分,可得 Chapman-Komolgorov 方程 (2) 更新过程,由得到: 猎取时刻的测量后,利用贝叶斯公式对先验概率密度进行更新,得到后验概率 假设只由决定,即因此其中,为归一化常数贝叶斯滤波以递推的形式给出后验(或滤波)概率密度函数的最优解。目标状态的最优估量值可由后验(或滤波)概率密度函数进行计算。通常根据极大后验(MAP)准则或最小均方误差(MMSE)准则,将具有极大后验概率密度的状态或条件均值作为系统状态的估量值,即 贝叶斯滤波需要进行积分运算,除了一些特别的系统模型(如线性高斯系统,有限状态的离散系统)之外,对于一般的非线性、非高斯系统,贝叶斯滤波很难得到后验概率的封闭解析式。...