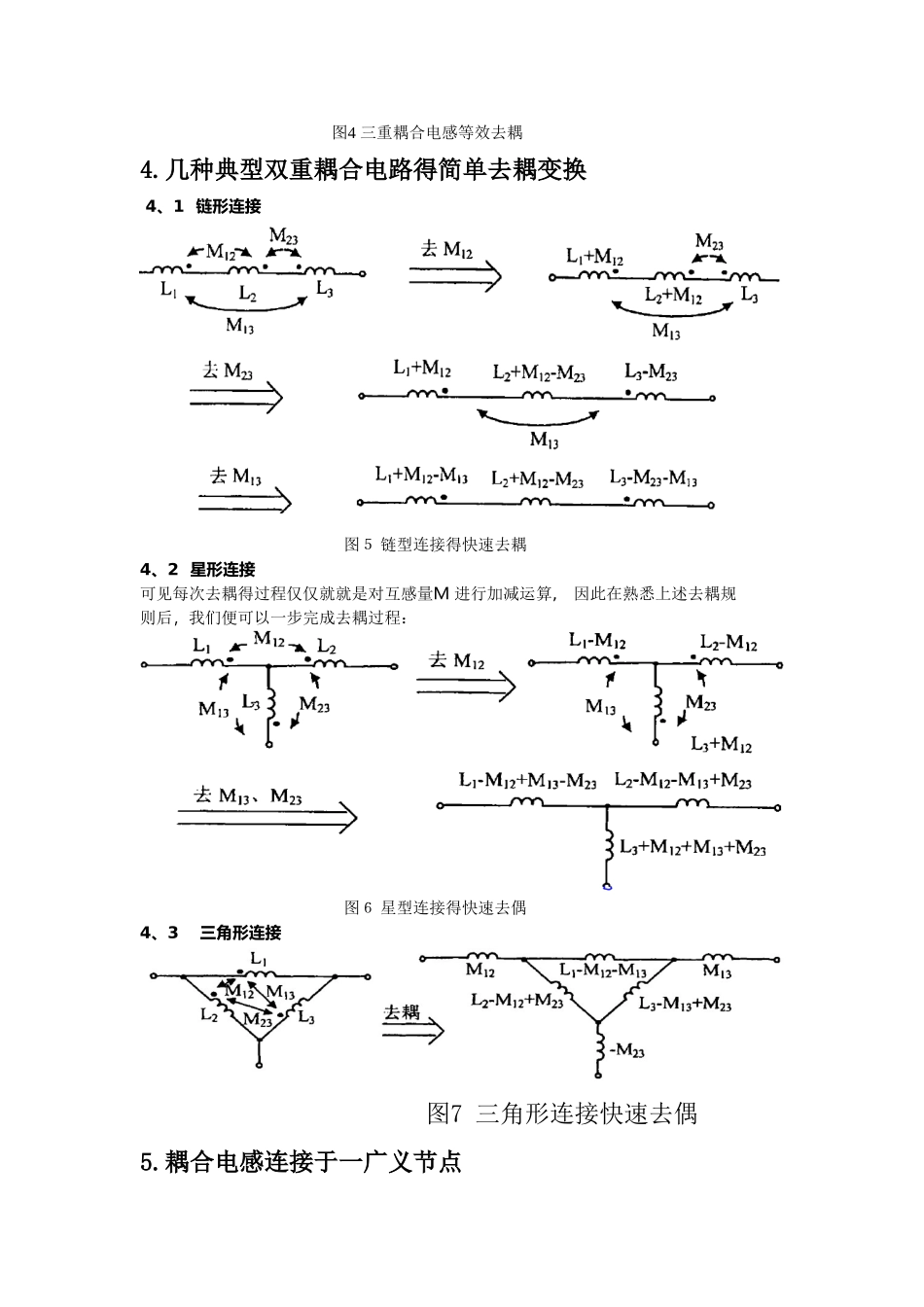
耦合电感得去耦等效方法得讨论王胤旭 509 0 309291陈琦然 5090309 30 6杨衎 50 9 030 9摘要:本文主要讨论有公共连接点得两个耦合电感得简单去耦等效方法以及由此衍生得两个特例--耦合电感得串联与并联。并讨论多重耦合电感得去耦相对独立性以及某些含有复杂耦合电感电路得快速去耦等效方法。1.有公共连接点得耦合电感得去耦等效图示电路中, 耦合电感L1与L2 有一公共连接点N, 根据耦合电感得性质, 可得如下方程:对于节点N有KCL方程:上面两式整理得:故可得其等效去耦电路如图2所示。 图1 耦合电感图2 等效去耦后得电感上述去耦过程可以用文字表述如下:1)设互感为M 得两耦合电感具有公共得连接点(假设其同名端相连)且连接点处仅含有三条支路, 则其去耦规则为: 含有耦合电感得两条支路各增加一个电感量为- M 得附加电感; 不含耦合电感得另一条支路增加一个电感量为- M 得附加电感。若为非同名端连接,只需将上述电感量M改变符号即可。2)若连接处含有多条支路, 则可以通过节点分裂, 化成一个在形式上仅含三条支路得节点。2.两个特例----耦合电感得串联与并联2、 1 两耦合电感串联1)若同名端连接于同一节点(即电流从异名端流入), 则构成反接串联,计算公式:;2)若非同名端连接于同一节点(即电流从同名端流入), 则构成顺接串联,计算公式:;2、 2 两耦合电感得并联1)若同名端连接于同一节点, 则构成同侧并联,计算公式:;2)若非同名端连接于同一节点, 则构成异侧并联,计算公式:;3.多重耦合电感得去耦相对独立性独立性:在电路中, 若含有多个电感得多重耦合, 可以只对其中某一个或某几个互感进行去耦变换, 保留其它耦合不变, 则变换后得电路与原电路等效。亦即, 多重耦合电感在去耦变换时具有相对得独立性。证明:设电路中含有三个电感元件, 且两两耦合, 如( 图4) 所示, 则根据耦合电感得性质, 可以用图5 所示受控源电路等效。 图3 三重耦合电感 图4 三重耦合电感等效去耦4.几种典型双重耦合电路得简单去耦变换 4、1 链形连接 图5 链型连接得快速去耦4、2 星形连接可见每次去耦得过程仅仅就就是对互感量M 进行加减运算, 因此在熟悉上述去耦规则后,我们便可以一步完成去耦过程: 图6 星型连接得快速去偶4、3 三角形连接 图7 三角形连接快速去偶5.耦合电感连接于一广义节点 图1描述得就就是两个耦合电感连接于一个单节点得情形。若它们连接于一个广义节点, 如...