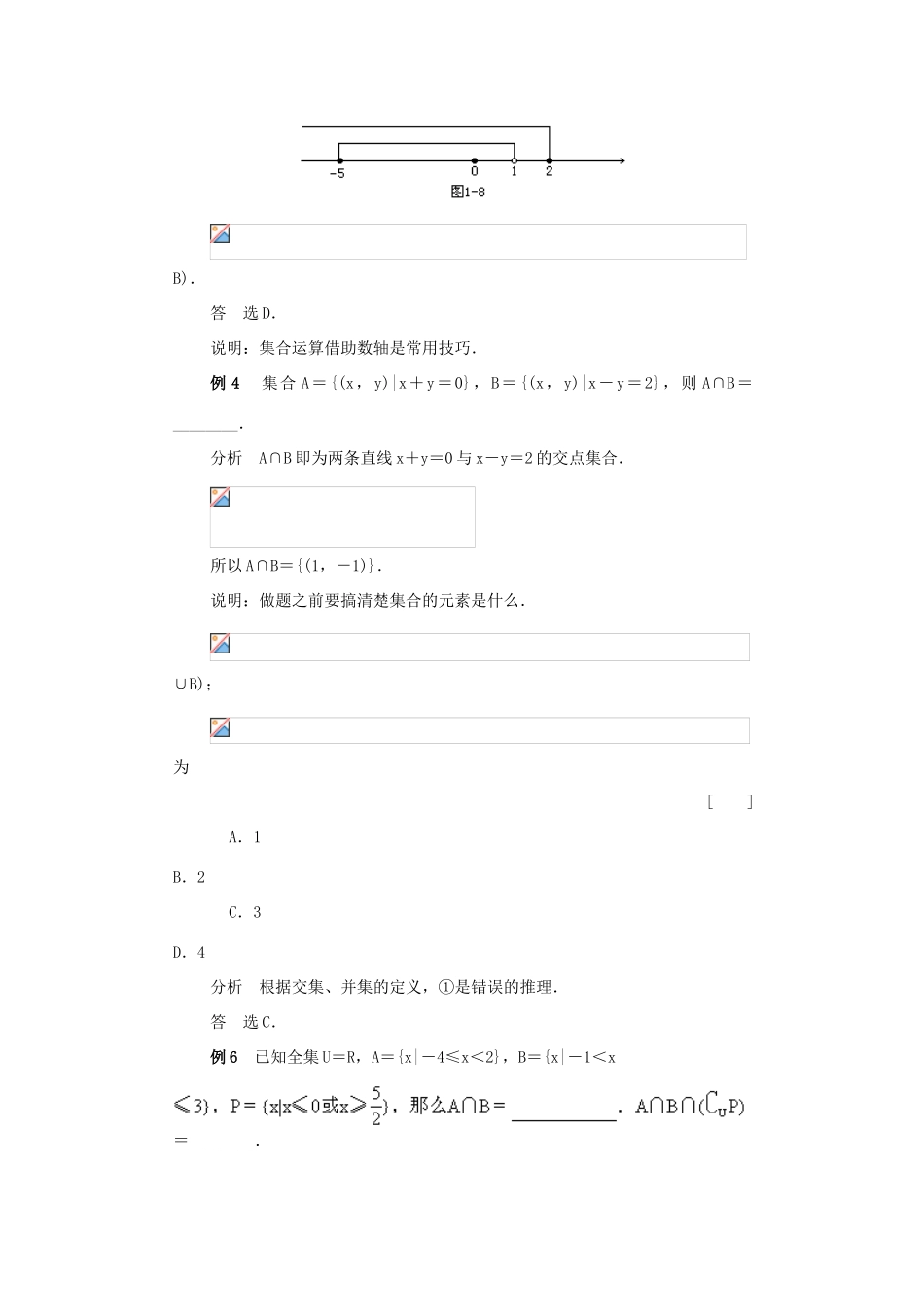
交集与并集例 1 已知 M={y|y=x2+1,x∈R},N={y|y=-x2+1,x∈R}则 M∩N 是[ ]A.{0,1} B.{(0,1)}C.{1} D.以上均不对分析 先考虑相关函数的值域.解 M={y|y≥1},N={y|y≤1},∴在数轴上易得 M∩N={1}.选 C.取值范围是[ ]A.m<4 B.m>4C.0<m<4 D.0≤m<4可得 0≤m<4.答 选 D.例 3 设集合 A={x|-5≤x<1},B={x|x≤2},则 A∪B=[ ]A.{x|-5≤x<1} B.{x|-5≤x≤2}C.{x|x<1} D.{x|x≤2}分析 画数轴表示B).答 选 D.说明:集合运算借助数轴是常用技巧.例 4 集合 A={(x,y)|x+y=0},B={(x,y)|x-y=2},则 A∩B=________.分析 A∩B 即为两条直线 x+y=0 与 x-y=2 的交点集合.所以 A∩B={(1,-1)}.说明:做题之前要搞清楚集合的元素是什么.∪B);为[ ]A.1 B.2C.3 D.4分析 根据交集、并集的定义,①是错误的推理.答 选 C.例 6 已知全集 U=R,A={x|-4≤x<2},B={x|-1<x=________.号的值.解 观察数轴得,A∩B={x|-1<x<2},A∩B∩(UP)={x|0<x<2}.例 7 设 A={x∈R|f(x)=0},B={x∈R|g(x)=0},[ ]A.C=A∪(UR) B.C=A∩(UB)C.C=A∪B D.C=(UA)∩B分析 依据分式的意义及交集、补集的概念逐步化归={x∈R|f(x)=0 且 g(x)≠0}={x∈R|f(x)=0}∩{x∈R|g(x)≠0}=A∩(UB).答 选 B.说明:本题把分式的意义与集合相结合.例 8 集合 A 含有 10 个元素,集合 B 含有 8 个元素,集合 A∩B 含有 3 个元素,则集合 A∪B 有________个元素.分析 一种方法,由集合 A∩B 含有 3 个元素知,A,B 仅有 3 个元素相同,根据集合元素的互异性,集合 A∪B 的元素个数为 10+8-3=15.另一种方法,画图 1-10 观察可得.答 填 15.例 9 已知全集 U={x|x 取不大于 30 的质数},A,B 是 U 的两个子集,且A∩(UB)={5,13,23},(UA)∩B={11,19,29},(UA)∩(UB)={3,7}求 A,B.分析 由于涉及的集合个数,信息较多,所以可以通过画图 1-11 直观地求解.解 U={2,3,5,7,11,13,17,19,23,29}用图形表示出 A∩(UB),(UA)∩B 及(UA)∩(UB)得U(A∪B)={3,7},A∩B={2,17},所以A={2,5,13,17,23},B={2,11,17,19,29}.说明:对于比较复杂的集合运算,可借助图形.例 10 设集合 A={x2,2x-1,-4},B={x-5,1-x,9},若 A∩B={9},求 A...