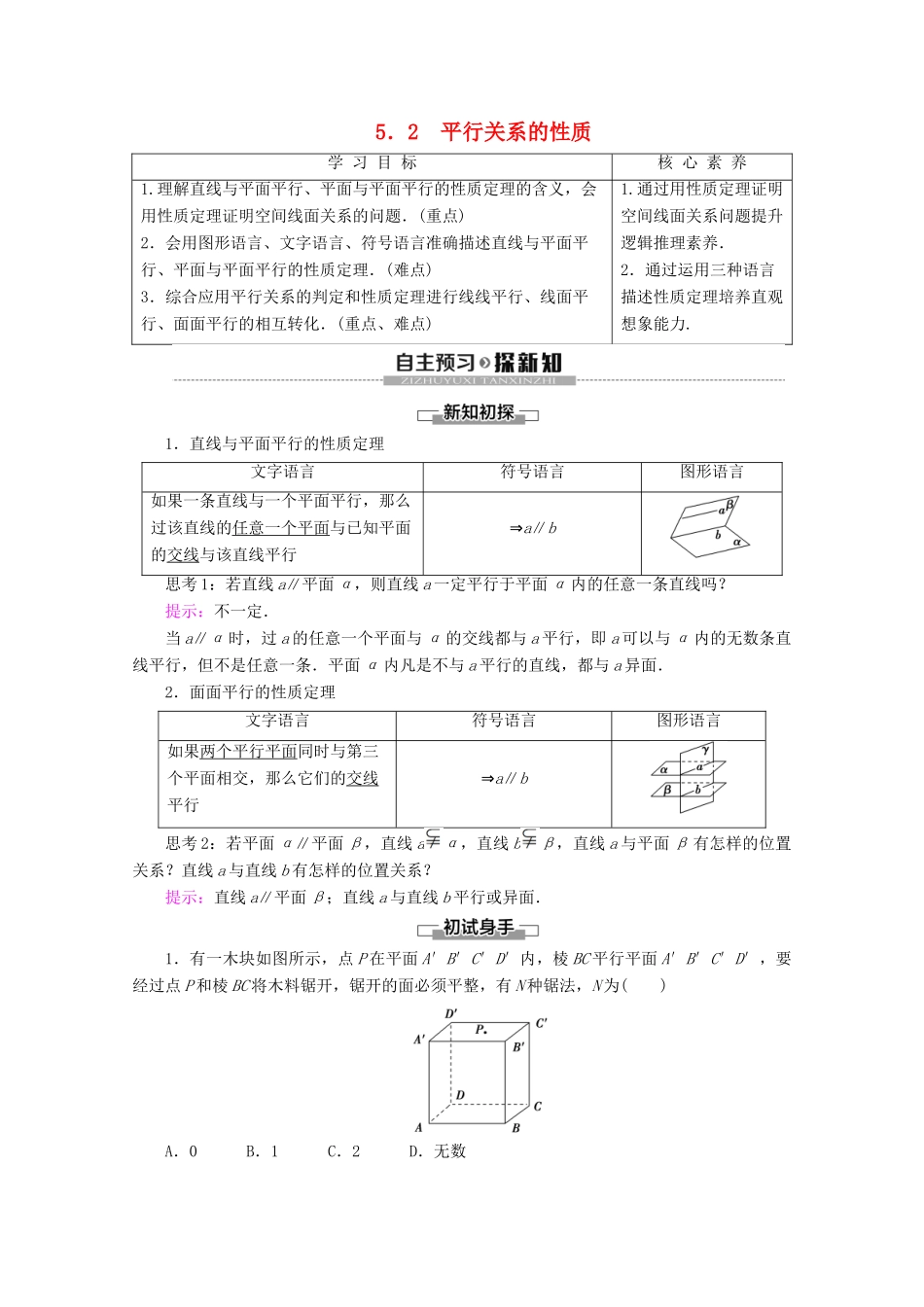
5.2 平行关系的性质学 习 目 标核 心 素 养1.理解直线与平面平行、平面与平面平行的性质定理的含义,会用性质定理证明空间线面关系的问题.(重点)2.会用图形语言、文字语言、符号语言准确描述直线与平面平行、平面与平面平行的性质定理.(难点)3.综合应用平行关系的判定和性质定理进行线线平行、线面平行、面面平行的相互转化.(重点、难点)1.通过用性质定理证明空间线面关系问题提升逻辑推理素养.2.通过运用三种语言描述性质定理培养直观想象能力.1.直线与平面平行的性质定理文字语言符号语言图形语言如果一条直线与一个平面平行,那么过该直线的任意一个平面与已知平面的交线与该直线平行⇒a∥b思考 1:若直线 a∥平面 α,则直线 a 一定平行于平面 α 内的任意一条直线吗?提示:不一定.当 a∥α 时,过 a 的任意一个平面与 α 的交线都与 a 平行,即 a 可以与 α 内的无数条直线平行,但不是任意一条.平面 α 内凡是不与 a 平行的直线,都与 a 异面.2.面面平行的性质定理文字语言符号语言图形语言如果两个平行平面同时与第三个平面相交,那么它们的交线平行⇒a∥b思考 2:若平面 α∥平面 β,直线 aα,直线 bβ,直线 a 与平面 β 有怎样的位置关系?直线 a 与直线 b 有怎样的位置关系?提示:直线 a∥平面 β;直线 a 与直线 b 平行或异面.1.有一木块如图所示,点 P 在平面 A′B′C′D′内,棱 BC 平行平面 A′B′C′D′,要经过点 P 和棱 BC 将木料锯开,锯开的面必须平整,有 N 种锯法,N 为( )A.0 B.1 C.2 D.无数B [ BC∥平面 A′B′C′D′,BC∥B′C′,在平面 A′B′C′D′上过 P 作 EF∥B′C′(图略),则 EF∥BC,∴沿过 EF,BC 所确定的平面锯开即可.又由于此平面唯一确定,∴只有一种方法,故选 B.]2.如图所示,在空间四边形 ABCD 中,E,F,G,H 分别是 AB,BC,CD,DA 上的点,EH∥FG,则 EH 与 BD 的位置关系是( )A.平行 B.相交C.异面 D.不确定A [ EH∥FG,EH平面 BCD,FG平面 BCD,∴EH∥平面 BCD, EH平面 ABD,平面 ABD∩平面 BCD=BD,∴EH∥BD.]3.六棱柱的两底面为 α 和 β,且 A∈α,B∈α,C∈β,D∈β,且 AD∥BC,则 AB 与CD 的位置关系为__________.平行 [ AD∥BC,∴A,B,C,D 共面,设为 γ,由题意知,α∩γ=AB,β∩γ=CD,又 α∥β,∴AB∥CD.]4.已知平面...