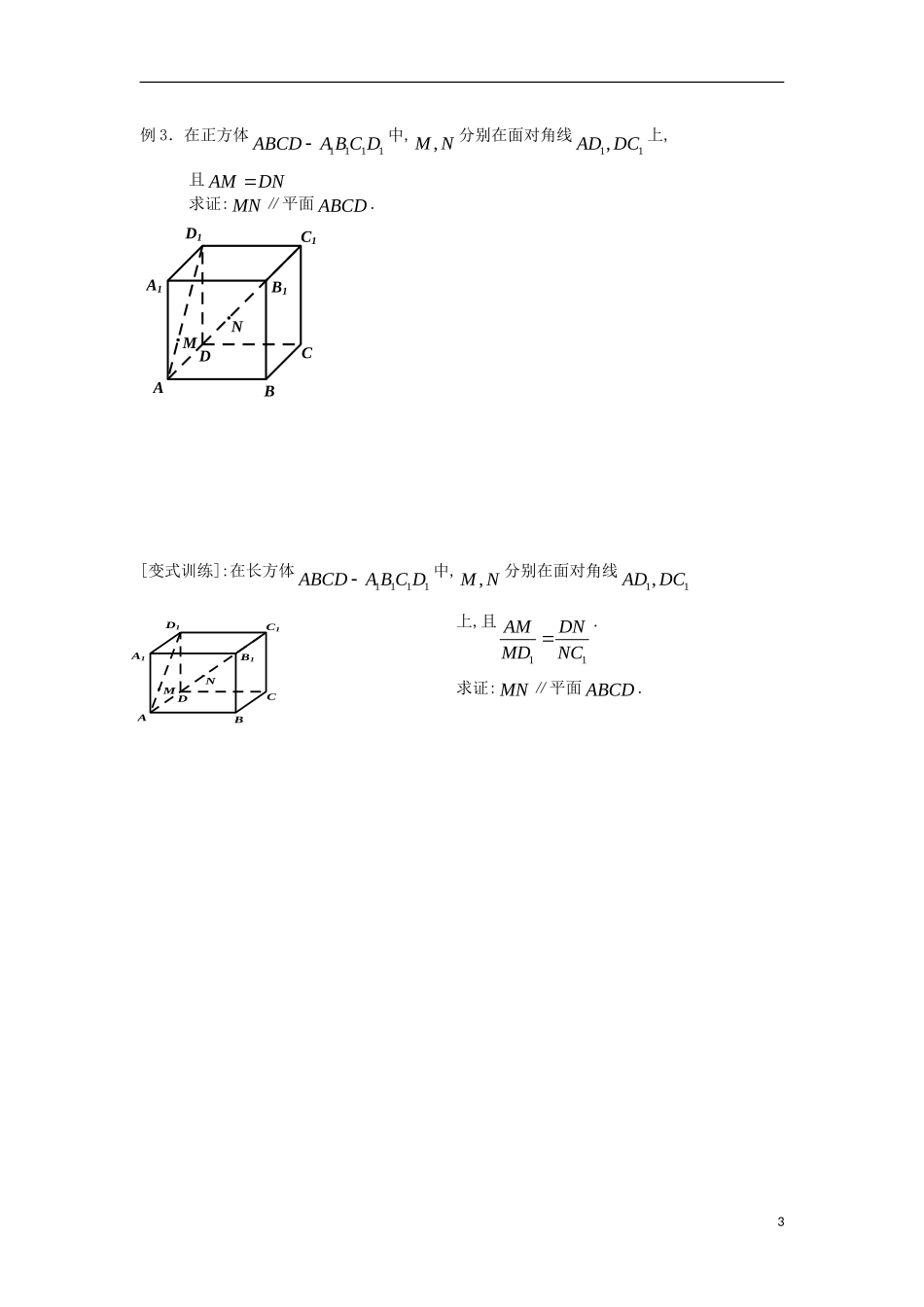
第 9 课时 直线与平面的位置关系(1)一、学习目标1. 直观感知直线与平面的三种位置关系;2. 初步掌握并能应用直线和平面平行的判定定理; 3. 体会类比思想在数学中的应用. 重点:直线与平面的三种位置关系;直线和平面平行的判定定理. 难点:直线和平面平行的判定定理的应用. 二、数学活动1.类比研究空间两条直线位置关系的方法写出直线与平面的几种位置关系,并在如图1所示的长方体1111ABCDA B C D中各举一例. 图1D1C1B1A1DCBA2.如图2 ,在长方体1111ABCDA B C D中, E 是棱1BB 的中点.分别写出直线1A E 、直线11A B 与平面 AC 的位置关系,并说明理由.3.下列命题中正确的有 .(填序号) ① 若一条直线不在某个平面内,则这条直线就与这个平面平行;② 若一条直线与某个平面内无数条直线平行,则这条直线就与这个平面平行;③ 过直线外一点有无数个平面与这条直线平行;④ 过平面外一点有无数条直线与这个平面平行.三、数学建构1.直线与平面的位置关系2.直线和平面平行的判定定理1E图2D1C1B1A1DCBA四、数学应用例 1 如图3 ,已知,E F 分别是三棱锥 ABCD的侧棱,AB AD 的中点.求证: EF ∥平面 BCD .例 2 在四棱锥 PABCD中, AB / / CD ,12DCAB, E 是 PB 的中点. 求证://EC平面 PAD .2图3FEDCBA例 3.在正方体1111ABCDA B C D中,,M N 分别在面对角线11,AD DC 上,且 AMDN求证: MN ∥平面 ABCD .D1C1CDB1A1ABNM[变式训练]:在长方体1111ABCDA B C D中,,M N 分别在面对角线11,AD DC上,且11AMDNMDNC.求证: MN ∥平面 ABCD .3D1C1CDB1A1ABNM五、巩固与小结《必修二》P35 练习 T3、T4、T5小结:4